Алгоритм обучения однослойной нейронной сети

Обучение нейронной сети происходит на некоторой обучающей выборке, для каждого образца которой определяются и сравниваются с желаемыми значениями все текущие выходы. Если разница недопустима, то веса изменяются. Концом обучения считается ситуация, когда общая ошибка на всех образцах допустима.

Рассмотрим обучение линейной однослойной сети, представленной на рис. 4.10.

Структура обучающей выборки -

Х = (Х₁, Х₂,..., Х_n), O = (O₁, O₂,..., O_m).

Пусть для обучения нам представлена выборка: Х^K, Y^K, K =1,... K, O {1,0}.

Приведем описание алгоритма обучения по шагам.

1. Введём к = 1; к -- номер образца.

2. Случайным образом инициализируем матрицу весов W_ij;

Е = 0, где Е - ошибка.

3. Начнем обучение (на модели), для чего просчитаем все выходы

для любого О_i.

4. Рассчитаем разницу между текущими и желаемыми значениями выходов, т.е. вычислим (Y_i - O_i), для каждого i.

5. Изменим веса по правилу

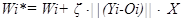для каждого W_i, Y_i.

6. Вычислим накопленную ошибку 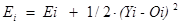, выберем следующий образец из обучающей выборки к = к + 1.

7. Проанализируем текущий результат. Если к K, то следует учесть ошибку. Если значение ошибки Е меньше заданного уровня , то достигнут конец обучения. Если накопленная ошибка больше , то установим к = 1, Е = 0 и вернемся к шагу 3, т. е. продолжим обучение.

Доказана теорема о сходимости алгоритма обучения однородной нейросети. Если задача линейносепарабельна, то алгоритм обучения однослойной нейросети сходится за конечное число шагов.

Дата добавления: 2014-01-11