Точечные оценки числовых характеристик и параметров

Статистической оценкой 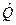параметра Q распределения называется приближенное значение параметра, вычисленное по результатам эксперимента (по выборке).

Точечной называется оценка, определяемая одним числом.

Оценка 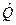называется состоятельной, если при увеличении объема выборки n она сходится по вероятности к значению параметра Q:

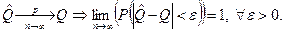
Оценка 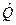называется несмещенной, если ее математическое ожидание точно равно параметру Q для любого объема выборки:

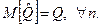
Несмещенная оценка 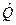является эффективной, если ее дисперсия минимальна по отношению к дисперсии любой другой оценки этого параметра.

Состоятельная несмещенная оценка математического ожидания, называемая выборочным средним 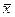, вычисляется по формуле

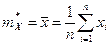. (54.7)

Числовые характеристики :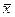

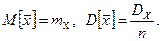
Состоятельная несмещенная оценка дисперсии равна

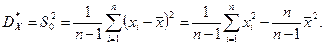(54.8)

Числовые характеристики :

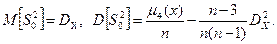
Состоятельная несмещенная оценка среднего квадратического отклонения:

(54.9)

Состоятельная оценка начального момента k-го порядка определяется по формуле

(54.10)

Состоятельная оценка центрального момента k-го порядка равна

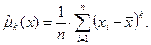(54.11)

Несмещенная состоятельная и эффективная оценка вероятности случайного события A в схеме независимых опытов Бернулли:

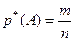(54.12)

где m - число опытов, в которых произошло событие A;

п - число проведенных опытов.

Числовые характеристики :

Для вычисления оценок параметров распределения чаще всего применяются методы моментов и максимального правдоподобия.

Суть метода моментов заключается в следующем. Пусть имеется выборка 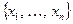независимых значений случайной величины с известным законом распределения и m неизвестными параметрами . Последовательность вычислений следующая:

1. Вычислить значения m начальных и/или центральных теоретических моментов

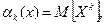
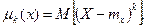
2. Определить m соответствующих выборочных начальных 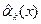и/или центральных 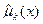моментов по формулам (54.10), (54.11).

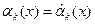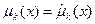3. Составить и решить относительно неизвестных параметров систему из m уравнений, в которых приравниваются теоретические и выборочные моменты. Каждое уравнение имеет вид или . Найденные корни являются оценками 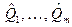неизвестных параметров.

Замечание. Часть уравнений может содержать начальные моменты, а оставшаяся часть - центральные.

Согласно методу максимального правдоподобия оценки 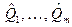получаются из условия максимума по параметрам 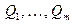положительной функции правдоподобия .

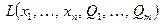Если случайная величина X непрерывна, а значения независимы, то

.

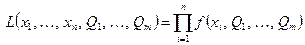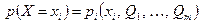Если случайная величина X дискретна и принимает независимые значения с вероятностями , то функция правдоподобия равна

.

Система уравнений согласно этому методу может записываться в двух видах:

или

.

Найденные корни выбранной системы уравнений являются оценками неизвестных параметров .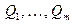

Пример 54.3. Случайная величина X распределена по равномерному закону, т.е.

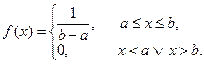
Необходимо определить оценки параметров a и b.

Решение. Для данного закона распределения определяем теоретические выражения двух (по числу неизвестных параметров) моментов:

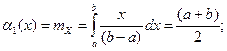
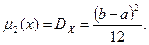
По исходной выборке определяем оценки этих же моментов 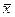и по формулам (54.7) и (54.8) соответственно. Составляем систему их двух уравнений:

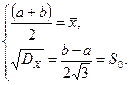
Решив ее относительно неизвестных параметров a и b, получим оценки:

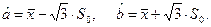
Пример 54.4. Пусть – независимые значения случайной величины X, распределенной по экспоненциальному закону, т.е.

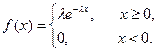
Необходимо получить оценку параметра 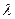методом максимального правдоподобия.

Решение. Функция правдоподобия имеет вид

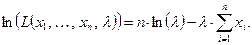
Далее записываем уравнение

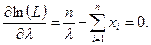
Решив его, получаем выражение для оценки параметра :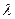

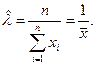
Дата добавления: 2014-01-13