Властивості основної задачі ЛП. Геометричне тлумачення задачі ЛП

Перепишемо задачу (4)-(7) у векторній формі: знайти максимум функції

(10)

за умов

, (11)

, (12)

де , 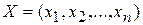; 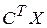– скалярний добуток; и 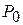- -мірні вектор-стовпчики, що складаються з коефіцієнтів при невідомих та вільних членах системи рівнянь задачі:

; ; ; …; .

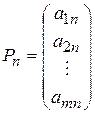Визначення 7. План 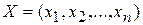називається опорним планом основної задачі ЛП, якщо система векторів 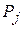, що входить у розклад (11) з позитивними коефіцієнтами , лінійно незалежна.

Визначення 8. Опорний план називається невиродженим, якщо він містить рівно позитивних компонент, у протилежному випадку він називається виродженим.

Властивості основної задачі ЛП (4)-(7) тісним чином пов’язані з властивостями опуклих множин.

Визначення 9. Нехай 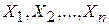- довільні точки евклідового простору 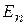. О пуклою лінійною комбінацією цих точок називається сума 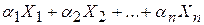, де - довільні невід’ємні числа, сума яких дорівнює 1: , .

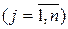Визначення 10. Множина називається опуклою, якщо разом з двома будь-якими своїми точками вона містить і їх довільну опуклу лінійну комбінацію.

Визначення 11. Точка опуклої множини називається кутовою, якщо вона не може бути представлена у вигляді опуклої лінійної комбінації будь-яких двох інших різних точок даної множини.

Теорема 1. Множина планів основної задачі ЛП являється опуклою (якщо вона не пуста).

Визначення 12. Непуста множина планів основної задачі ЛП називається багатокутником розв’язків, а будь-яка кутова точка багатокутника рішень – вершиною.

Теорема 2. Якщо основна задача ЛП має оптимальний план, то максимальне значення цільова функція задачі набуває в одній з вершин багатокутника розв’язків. Якщо максимальне значення цільова функція задачі набуває більш ніж в одній вершині, то вона набуває його у всякій точці, що є опуклою лінійною комбінацією цих вершин.

Теорема 3. Якщо система векторів 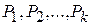у розкладі (11) лінійно незалежна і є такою, що

, (13)

де всі 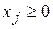, то точка є вершиною багатокутника розв’язків.

Теорема 4. Якщо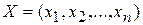- вершина багатокутника розв’язків, то вектори 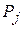, що відповідають позитивним у розкладі (11) лінійно незалежні.

Сенс теорем 1-3 має досить просту геометричну інтерпретацію, котру покладено в основу так званого геометричного методу вирішення задачі ЛП. Його доцільно застосовувати для розв’язку задач низької розмірності .

Алгоритм розв’язку задачі ЛП (4)-(7) геометричним методом для випадку .

1. Будуються прямі, рівняння яких отримують у результаті заміни в обмеженнях (5) та (7) знаків нерівностей на знаки точних рівностей.

2. Знаходять напівплощини, що визначаються кожним з обмежень задачі.

3. Знаходять багатокутник розв’язків.

4. Будують вектор .

5. Будують пряму , що проходить через багатокутник розв’язків.

6. Пересувають пряму у напрямку вектора , у результаті чого знаходять або точку (точки), в якій цільова функція набуває максимального значення, або встановлюють необмеженість зверху функції на множині планів.

7. Визначають координати точки максимуму функції й обчислюють значення цільової функції в цій точці.

Приклад 2 [3].

(14)

.

Розв’язок.

1. Будуємо прямі, рівняння яких отримують у результаті заміни в обмеженнях (14) знаків нерівностей на знаки точних рівностей.

2. Знаходимо напівплощини, що визначаються кожним з обмежень задачі.

3. Знаходимо багатокутник розв’язків (рис. 2).

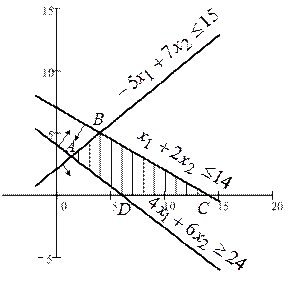Рис. 2

Рис. 3

4. Будуємо вектор .

5. Будуємо пряму 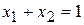, що проходить через багатокутник розв’язків. Для простоти побудови .

6. Пересуваємо пряму 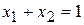у напрямку вектора 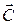, в результаті чого знаходимо точку мінімуму – А, та максимуму – С.

7. Визначаємо координати точки мінімуму 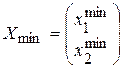А шляхом розв’язку системи лінійних рівнянь

та обчислюємо значення цільової функції в цій точці:

.

Визначаємо координати точки максимуму 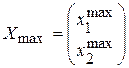С шляхом розв’язку системи лінійних рівнянь

та обчислюємо значення цільової функції в цій точці:

.

Література

1. Костылева М. Е., Церков А. В., Козлова О. В., Семенов Г. Е. Линейное программирование и прикладне задачи: Учебное пособие. М.: «МАТИ»-РГТУ им. К. Э. Циолковского, 2001. 113 с.

2. Ларіонов Ю. І., Левикін В. М., Хажмурадов М. А. Дослідження операцій в інформаційних системах: Навч. посібник. – 2-е вид. – Харків: Компанія СМІТ, 2005. – 364 с.

3. Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. Пособие для студентов эконом. спец. вузов. – М.: Высш. шк., 1986. – 319 с.

Дата добавления: 2014-01-13