
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пряма та двоїста задачі ЛП
|
|
|
|
Тема 1 Лінійне програмування
(8 г. – 4 лекції)
Лекція 3 (2 г.)
2.3 Двоїста(спряжена) задача ЛП
2.3.1Пряма та двоїста задачі ЛП
2.3.2 Зв’язок між розв’язками прямої та двоїстої задач
2.3.3Пошук розв’язку двоїстої задачі
2.3.4 Економічне тлумачення двоїстих задач*
2.3.5 Аналіз робастності двоїстих оцінок*
2.3.6 Двоїстий симплекс-метод*
2.3 Двоїста задача ЛП
Будь-якій задачі ЛП можна певним чином зіставити так звану двоїсту задачу по відношенню до даної.
Запишемо умову прямої задачі ЛП:
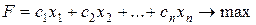 , за умов (26)
, за умов (26)
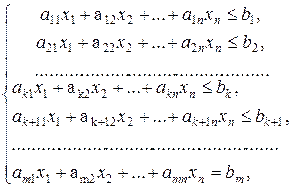 , (27)
, (27)
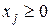 (
( ). (28)
). (28)
Визначення 14. Задача, яка полягає в находженні мінімального значення функції
 , за умов (29)
, за умов (29)
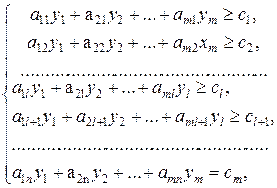 , (30)
, (30)
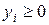 (
(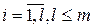 ), (31)
), (31)
називається двоїстою по відношенню до задачі (26)-(28).
Алгоритм побудови двоїстої задачі:
1. Цільова функція прямої задачі (26)-(28) задається на максимум, а цільова функція двоїстої задачі (29)-(31) задається на мінімум.
2. Матриця коефіцієнтів двоїстої задачі – це транспонована матриця коефіцієнтів прямої задачі.
3. Кількість змінних двоїстої задачі (29)-(31) дорівнює кількості співвідношень (27) прямої, тобто 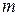 . Кількість обмежень у системі (30) – кількості змінних у прямій задачі, тобто
. Кількість обмежень у системі (30) – кількості змінних у прямій задачі, тобто  .
.
4. Вектор коефіцієнтів цільової функції і вектор правих частин у двоїстій задачі міняються містами по відношенню до прямої, тобто  .
.
5. Якщо змінна 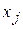 прямої задачі може приймати тільки позитивні значення, то
прямої задачі може приймати тільки позитивні значення, то  та умова у системі (30) двоїстої задачі буде нерівністю виду «
та умова у системі (30) двоїстої задачі буде нерівністю виду «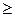 ». Якщо змінна
». Якщо змінна 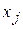 може приймати як позитивні, так і відмінні значення, то
може приймати як позитивні, так і відмінні значення, то  та умова у системі (30) двоїстої задачі буде рівнянням. Якщо
та умова у системі (30) двоїстої задачі буде рівнянням. Якщо 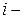 те співвідношення у системі (30) є нерівністю, то
те співвідношення у системі (30) є нерівністю, то 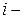 та змінна двоїстої задачі
та змінна двоїстої задачі 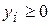 . У протилежному випадку змінна
. У протилежному випадку змінна  може набувати як позитивних, так і від’ємних значень.
може набувати як позитивних, так і від’ємних значень.
Існують два види моделей двоїстих задач: симетричні і несиметричні:
Симетричні:
Вихідна
1.  , ,
 , ,

| Двоїста
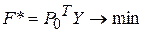 , ,
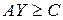 , ,
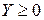
|
2. 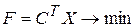 , ,
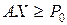 , ,

| 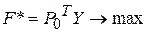 , ,
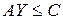 , ,
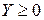
|
Несиметричні:
Вихідна
1.  , ,
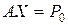 , ,

| Двоїста
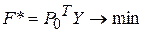 , ,
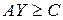 , ,
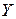 – будь-які – будь-які
|
2. 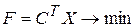 , ,
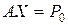 , ,

| 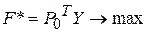 , ,
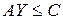 , ,
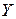 – будь-які – будь-які
|
Приклад 4 [3]. Скласти двоїсту задачу по відношенню до наступної задачі:
 (32)
(32)
за умов
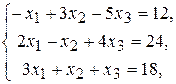 (33)
(33)
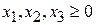 . (34)
. (34)
Двоїста задача має вигляд:
 ,
,

 - будь-які.
- будь-які.
Приклад 5. Скласти двоїсту задачу по відношенню до наступної задачі:
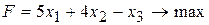 (35)
(35)
за умов
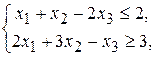 (36)
(36)
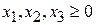 . (37)
. (37)
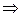
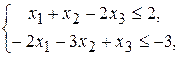
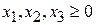 .
.
Двоїста задача має вигляд:
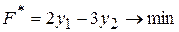 (38)
(38)
за умов
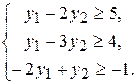 (39)
(39)
 .
.
Приклад 6. Скласти двоїсту задачу по відношенню до наступної задачі:
 (40)
(40)
за умов
 (41)
(41)
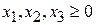 . (42)
. (42)
Двоїста задача має вигляд:
 (43)
(43)
за умов
 (44)
(44)

 – будь-яке. (45)
– будь-яке. (45)
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 1110; Нарушение авторских прав?; Мы поможем в написании вашей работы!