Пошук розв’язку двоїстої задачі

Припустимо, що за допомогою симплекс-методу знайдено оптимальний план 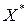задачі (46)-(48) і цей план визначається базисом, що створюється векторами .

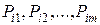Позначимо через 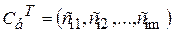вектор-рядок, складений з коефіцієнтів при невідомих в цільовій функції (46) задачі (46)-(48), через 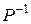– матрицю, зворотну до 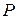, складену з компонент векторів 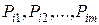базису. Тоді має місце наступне твердження.

Теорема 11. Якщо основна задача лінійного програмування має оптимальний план 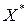, то 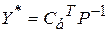є оптимальним планом двоїстої задачі.

Приклад 7. Доданоїзадачі скласти двоїсту і знайти розв’язок обох задач: 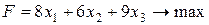(51)

за умов

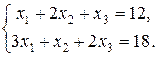(52)

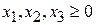. (53)

Двоїста задача має вигляд:

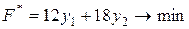(54)

за умов

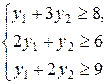(55)

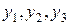- будь-які. (56)

Розв’язок.

1. Розв’яжемо першу задачу симлекс-методом, попередньо ввівши дві штучні,базисні змінні 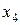та :

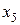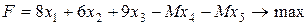(57)

за умов

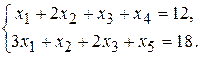(58)

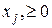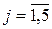, . (59)

Остання симплекс-таблиця має вигляд:

Базис		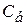План				-М	-М

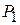
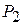
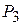
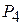
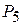
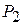
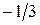
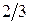
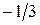
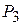
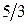
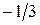
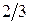
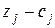
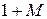
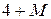
Оптимальний план першої задачі:

.

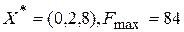Розв’язок двоїстої задачі знаходимо з гідно з теоремою 8 за формулою:

,

, .

,

.

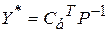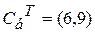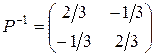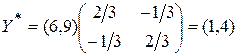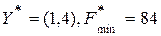
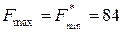2.3.4 Економічне тлумачення двоїстих задач*

2.3.5 Аналіз робастності двоїстих оцінок*

2.3.6 Двоїстий симплекс-метод*

Література

1. Костылева М. Е., Церков А. В., Козлова О. В., Семенов Г. Е. Линейное программирование и прикладне задачи: Учебное пособие. М.: «МАТИ»-РГТУ им. К. Э. Циолковского, 2001. 113 с.

2. Ларіонов Ю. І., Левикін В. М., Хажмурадов М. А. Дослідження операцій в інформаційних системах: Навч. посібник. – 2-е вид. – Харків: Компанія СМІТ, 2005. – 364 с.

3. Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. Пособие для студентов эконом. спец. вузов. – М.: Высш. шк., 1986. – 319 с.

Дата добавления: 2014-01-13