Методи безпосереднього пошуку оптимуму. Вступ

Розв’язок рівняння (2.3) потребує попереднього обчислення похідної досліджуваної функції. Це не завжди зручно, особливо у випадках програмної реалізації розв’язку задачі оптимізації. Існують інші чисельні підходи, які дозволяють безпосередньо обчислювати мінімум функції 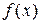на заданому відрізку 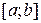без пошуку похідної. Розглянемо такі методи.

2.3.3.1 Метод поділу навпіл

На відрізку 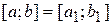вибирають дві точки (рис. 2.4)

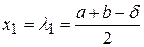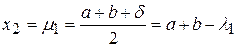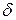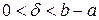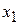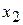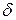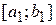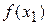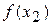, , де – задана наперед константа, що характеризує точність обчислень . Точки та відрізняються на величину і майже ділять відрізок навпіл. Далі обчислюються значення функції та . Якщо , то відрізок 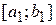звужується до відрізку 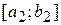таким чином: 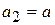, 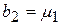. Інакше, якщ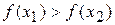о , то 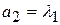, 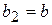. Довжина відрізку 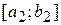, що містить мінімум функції буде дорівнювати .

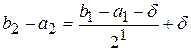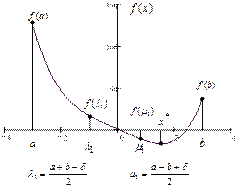
Рис. 2.4 До пояснення методу ділення навпіл

На 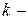ій ітерації маємо відомий відрізок , що містить точку мінімуму. Нехай його довжина

, .

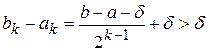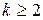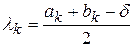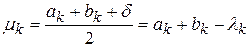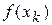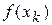Тоді , . Далі обчислюються значення функції та . Якщо 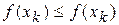, то відрізок звужується до відрізку 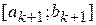таким чином: 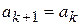, 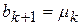. Інакше, якщ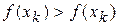о , то 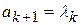, 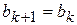. Довжина відрізку 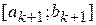, що містить мінімум функції, буде дорівнювати

.

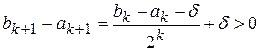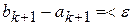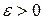Ітераційний процес припиняється за умови , де – задана наперед точність.

2.3.3.2 Метод золотого перетину* (самостійно згідно з [2])

Метод золотого перетину аналогічний методу поділу навпіл. Але на відміну від методу поділу навпіл, поділ відрізку здійснюється таким чином, що відношення довжини всього відрізку до довжини більшої частини дорівнює відношенню більшої частини до меншої. Можна показати, що швидкість збіжності такого підходу більше, ніж у методу поділу навпіл. Також метод золотого перетину, як і метод Фібоначчі, на кожній ітерації, починаючи з другої, потребує тільки одного обчислення значення функції.

2.3.3.3 Метод Фібоначчі* (самостійно згідно з [2])

На відміну від методів поділу навпіл та золотого перетину, метод Фібоначчі потребує заданої кількості 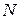обчислень значень функції.

Література

1. Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. Пособие для студентов эконом. спец. вузов. – М.: Высш. шк., 1986. – 319 с.

2. Банди Б. Методы оптимизации. Вводный курс. – Пер. с англ. - М.: Радио и связь, 1988 (Brian D. Bunday, BASIC OPTIMISATION METHODS).

Дата добавления: 2014-01-13