Количественное измерение

При количественном измерении определяют интенсивность аналитического сигнала, т. е. числовое значение свойства, связанное с количеством или содержанием анализируемого компонента.

В гравиметрическом анализе интенсивностью аналитического сигнала является масса высушенного или прокаленного осадка, в титриметрическом – объем раствора, израсходованный на реакцию, в фотометрическом – интенсивность окраски раствора (оптическая плотность) и т.д.

В случае необходимости обнаружения какого-либо компонента обычно фиксируют появление аналитического сигнала – появление осадка, окраски, линии в спектре и т.д. Появление аналитического сигнала должно быть надежно зафиксировано.

При измерении аналитического сигнала учитывают наличие полезного аналитического сигнала, являющегося функцией содержания определяемого компонента, и аналитического сигнала фона, обусловленного примесями определяемого компонента и мешающими компонентами в растворах, растворителях и матрице образца, а также «шумами», возникающими в измерительных приборах, усилителях и другой аппаратуре. Эти шумы не имеют отношения к определяемому компоненту, но накладываются на его собственный аналитический сигнал. Задача аналитика состоит в том, чтобы максимально снизить величину аналитического сигнала фона и сделать минимальными его колебания. Обычно аналитический сигнал фона учитывают при проведении контрольного (холостого) опыта, когда через все стадии химического анализа проводится проба, не содержащая определяемого компонента. Полезным сигналом при этом будет аналитический сигнал, равный разности измеренного аналитического сигнала и аналитического сигнала фона.

По результатам количественного измерения с помощью уравнения связи рассчитывают содержание определяемого элемента в пробе.

Уравнение связи выражает количественную зависимость между интенсивностью аналитического сигнала (измеряемой величиной) и содержанием или количеством анализируемого компонента:

Р = f(c),

где Р — интенсивность аналитического сигнала; с — концентрация.

Вид функциональной зависимости определяется главным образом особенностями аналитического сигнала. Зависимость может быть линейной, логарифмической и т. д. В качестве уравнения связи могут быть использованы как теоретически обоснованные соотношения, так и эмпирически найденные зависимости между интенсивностью сигнала и концентрацией.

Обычно при этом используют методы градуировочного графика, стандартов или добавок. Описанные в литературе другие способы определения содержания компонента, как правило, являются модификацией этих трех основных методов.

Наиболее распространен метод градуировочного графика. При этом в координатах аналитический сигнал – содержание компонента строят график с использованием образцов сравнения с различным и точно известным содержанием определяемого компонента. Затем, измерив величину аналитического сигнала в анализируемой пробе, находят содержание определяемого компонента по градуировочному графику (рис. 1):

Рис.1. Метод градуировочного графика

В методе стандартов измеряют аналитический сигнал в образце сравнения (эталонном образце) с известным содержанием компонента и в анализируемой пробе:

у _эт = Sc _эт и у_х = Sc_x,

где S — коэффициент пропорциональности.

Если определенное в идентичных условиях значение S заранее известно, то обычно применяют соотношение у _эт / у_х = с _эт / с_x, откуда

Иногда используют 2 эталонных образца, в которых содержание компонента отличается от предполагаемого в анализируемой пробе в одном случае в меньшую, в другом – в большую сторону. Этот вариант метода стандартов называют иногда методом ограничивающих растворов. Содержание определяемого компонента рассчитывают по формуле

В тех случаях, когда при определении малых количеств компонента нужно учесть влияние матрицы образца на величину аналитического сигнала, часто используют метод добавок – расчетный и графический.

При определении содержания расчетным методом берут 2 аликвоты раствора анализируемой пробы. В одну из них вводят добавку определяемого компонента известного содержания. В обеих пробах измеряют аналитический сигнал – у_х и у_{х +доб}. Неизвестную концентрацию определяемого компонента рассчитывают по формуле:

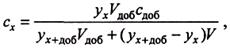
где V _доб и с _доб – объем и концентрация добавленного раствора определяемого компонента; V – аликвота анализируемой пробы.

При определении содержания компонента графическим методом берут п аликвот анализируемой пробы: 1, 2, 3,..., п. В аликвоты 2, 3,..., п вводят известные, возрастающие количества определяемого компонента. Во всех аликвотах измеряют аналитический сигнал и строят график в координатах аналитический сигнал – содержание определяемого компонента, приняв за условный нуль содержание определяемого компонента в аликвоте без добавки (аликвота 1). Экстраполяция полученной прямой до пересечения с осью абсцисс дает отрезок, расположенный влево от условного нуля координат, величина которого в выбранном масштабе и единицах измерения соответст­вует искомому содержанию (с_х) определяемого компонента (рис. 2).

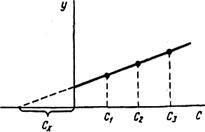
Рис.2. Метод добавок

Метод стандартов и метод добавок применимы для линейной градуировочной функции. Метод градуировочного графика допускает использование как линейной, так и нелинейной функций аналитический сигнал – содержа­ние. В последнем случае требуется большее число экспериментальных данных и результат определения содержания компонента бывает, как правило, менее точным.

Для построения градуировочного графика, наилучшим образом удовлетворяющего экспериментальным данным, обычно используют метод наименьших квадратов (МНК).

Основное положение МНК утверждает, что если для каждой из т экспериментальных точек провести на оптимальную кривую прямые, параллельные оси ординат, то для оптимальной (теоретической) кривой сумма квадратов отклонений точек от кривой (δ _i) должна быть минимальной, т. е.

В химическом анализе чаще всего используют прямолинейные градуировочные графики, построенные для определенного диапазона определяемых содержаний, т. е. в области значений, предусмотренных данной методикой.

Уравнение прямой можно записать в виде у = а + bх. Если имеется т экспериментальных точек (х₁у₁, х₂y₂, …, х_ту_т), то, используя постулат МНК, можем найти параметры а и b прямой, наилучшим образом удовлетворяющей экспериментальным данным:

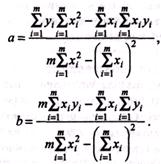
Параметры а и b тем точнее и, следовательно, построенный градуировочный график тем ближе к теоретическому, чем в более широком диапазоне определяемых содержаний строится график и чем большее число образцов сравнения (эталонов) т было взято для его построения.

Во всех методах определения неизвестного содержания компонента используют функциональную зависимость у = Sx.

Коэффициент чувствительности S (иногда его называют просто чувствительность) характеризует отклик аналитического сигнала на содержание компонента. Коэффициент чувствительности – это значение первой производной градуировочной функции при данном определенном содержании. Для прямолинейных градуировочных графиков – это тангенс угла наклона прямой (см. рис. 1):

Чем больше коэффициент чувствительности S, тем меньшие количества компонента можно обнаруживать и определять, получая один и тот же аналитический сигнал. Чем выше S, тем точнее можно определить одно и то же количество вещества.

Во всех рассмотренных способах используют образцы сравнения (эталоны), т. е. образцы, пробы, растворы с точно установленным содержанием компонента. Методы анализа, использующие образцы сравнения – это так называемые относительные методы химического анализа.

Абсолютных (безэталонных) методов в аналитической химии немного – например, ме­тоды гравиметрии, прямой кулонометрии, некоторые варианты радиохими­ческих методов.

Образцы сравнения для относительных методов анализа могут быть приготовлены из химически чистых, устойчивых веществ известного состава (стандартные вещества). В этом случае содержание определяемого компонента вычисляют по химической формуле стандартного вещества. Возможно приготовление образцов сравнения в отдельной лаборатории, учреждении, отрасли, когда содержание компонента устанавливают разными методами, на разных приборах многие аналитики.

Наиболее надежные результаты получают, когда в качестве образцов сравнения используют стандартные образцы (СО) – специально приготовленные материалы, состав и свойства кото­рых достоверно установлены и официально аттестованы специальными государственными метрологическими учреждениями.

При проведении химического анализа обычно не ограничиваются единичным определением, а проводят несколько параллельных определений (как правило, 3 – 5) для одной и той же пробы в одинаковых условиях. Средний результат параллельных определений называют результатом анализа и обозначают через или 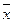. Отклонение результата анализа от истинного содержания определяемого компонента (с _ист, х _ист) называют погрешностью (или ошибкой) определения.

Наряду с обнаружением или определением содержания компонента важна оценка достоверности полученных результатов, погрешностей измерения.

Дата добавления: 2014-01-11