Правильность, воспроизводимость и точность анализа, среднее значение и стандартное отклонение

Случайные погрешности

Случайные погрешности не имеют определенного знака, и само название «случайные» указывает на отсутствие какой-либо закономерности в появлении погрешности этого типа.

Примером случайных погрешностей служат результаты параллельных анализов, которые почти всегда несколько отличаются один от другого, даже если все источники систематиче­ских погрешностей учтены с помощью соответствующих попра­вок.

Появление случайных погрешностей обычно рассматривают как случайное событие, и эти погрешности подвергают обработке на основе теории вероятности и математической статистики.

Правильностью измерений называют качество измерений, отражающее близость к нулю систематических погрешностей.

Сходимостью измерений называют качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях.

Более широкий смысл вкладывается в понятие «воспроизводимость».

Воспроизводимостью измерений называют качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (в разное время, разными методами и т. д.).

Точностью измерений называют качество измерений, отражающее близость их результатов к истинному значению измеряемой величины.

Высокая точность измерений соответствует малым погрешностям всех видов как систематическим, так и случайным.

Количественно точность может быть выражена обратной величиной модуля относительной погрешности. Например, относительная погрешность измерения характеризуется значением 0,01%, то точность будет равна 1/10^-4 = 10⁴.

Результат анализа, приближающийся к истинному содержанию компонента настолько, что может быть использован вместо него, следует называть действительным содержанием.

Из математической статистики известно, что наиболее вероятным и наилучшим значением измеряемой величины является математическое ожидание. Для серии из n дискретных измере­ний математическое ожидание М(х) определяется формулой:

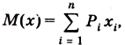
где x_i; — результат i -го измерения; Р_i — его вероятность.

В случае равноточных измерений:

соотношение переходит в

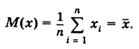
Таким образом, в случае равноточных измерений математическое ожидание совпадает с понятием среднего арифметического.

Положение о совпадении среднего арифметического с матема­тическим ожиданием строго относится к гипотетической генераль­ной совокупности, т. е. совокупности всех наблюдений, мыслимых при данных условиях. Арифметическое среднее этих наблюдений называют генеральным средним.

В аналитической химии число параллельных определений обычно невелико и совокупность по­лученных результатов называют выборочной совокупностью или случайной выборкой, а среднее значение результатов случайной выборки – выборочным средним в отличие от генерального.

Чем больше объем выборки, тем ближе среднее арифметическое к математическому ожиданию.

Методами статистического анализа можно по результатам случайной выборки оценить параметры генеральной совокупнос­ти и таким образом найти наиболее вероятное значение содержа­ния компонента в пробе.

Если x₁, x₂,..., х_п – результаты параллельных определений компонента в пробе одним и тем же методом, то среднее арифме­тическое будет равно:

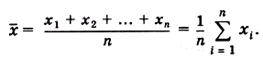
Например, в четырех параллельных определениях олова в бронзе фотометрическим методом в виде тиомочевинного комплекса бы­ли получены следующие результаты (w _Sn%): 4,80, 4,65; 4,84; 4,61. Тогда средним арифметиче­ским будет значение:

Для упрощения и удобства расчетов начало отсчета обычно смещают на некоторое разумно выбранное значение и вычисления проводят по формуле:

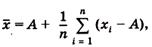
где А — произвольно выбранное значение, на которое смещается начало отсчета.

В данном случае принимаем А = 4,60 и рассчитываем х:

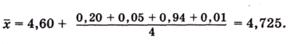
Среднее геометрическое ниже среднего арифметического. В среднем значении приведена одна «лишняя» значащая цифра по сравнению с исходными данными. Это сделано для того, чтобы не вносить погрешности за счет округления при проведении последующих расчетов с использованием среднего зна­чения. Однако не следует приводить и слишком много «лишних» цифр (3 – 4 и более), так как это вызывает дополнительные затраты времени на вычисления, не улучшая реальной точности результата. Нередко студенты автоматически записывают полностью все число, которое «выдает» компьютер или микрокалькулятор в результате расчета, что является, конечно, неприемлемым, посколь­ку не характеризует достигнутую точность.

Таким образом, во всех промежуточных вычислениях, включая расчет среднего арифме­тического, следует приводить на одну значащую цифру больше, чем число знаков в исходных данных.

Округляется только окончательный результат. Округление производится по специальным правилам и с учетом погрешности.

Если за последней округляемой стоит цифра 5, округляемую цифру оставляют без изменений (округление с уменьшением), а если больше 5, округляемую цифру увеличивают на единицу (округление с увеличением).

Например, 4,7252 округляют до 4,725, но 4,7257 округляют до 4,726.

Несколько сложнее правила округления, когда за последней округляемой цифрой стоит 5. Если за этой цифрой 5 нет более никаких цифр, то округляют до четной цифры, например, 4,7255 → 4,726, но 4,7245 → 4,724. Если за цифрой 5 имеется еще какая-либо отличная от нуля цифра, то округляют с увеличением, однако если 5 получено в результате округления, то округляют с уменьшением, т.е. 5 просто отбрасывают. Например, 4,72551 → 4,726, но 4,72548 → 4,7255 → 4,725.

При окончательном округлении результатов сначала округляют погрешность. Часто, но не всегда принимают во внимание, что, если первая цифра погрешности приводят две значащие цифры, а если к 9, – то одну.

Отдельные результаты анализа x₁, x₂,..., x_i рассеяны в неко­тором интервале значений от x_min до х_тах, называемом размахом варьирования R. Разность между отдельным результатом и сред­ним значением называют случайным отклонением или единич­ным отклонением или просто отклонением d:

Рассеяние случайной величины относительно среднего значе­ния характеризуется дисперсией S²:

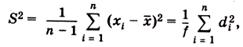
где f = n – 1 — число степеней свободы, определяемое как число независимых измерений за вычетом числа связей, наложенных на эту систему при обработке материала.

Если число наблюдений очень велико, величина S² стремится к некоторому постоянному значению σ², которое можно назвать статистическим пределом S². Строго говоря, этот предел и следует называть дисперсией измерений, а величина S² является выборочной дисперсией измерений.

Одно из важнейших свойств дисперсии, имеющее большое значение в теории погрешностей, передается уравнением

S²(x + y) = S²(x) + S²(y)

т. е. дисперсия суммы случайных величин равна сумме их дисперсий. Это означает, например, что при расчете погрешности суммы случайных величин следует оперировать непосредственно с их дисперсиями.

Однако дисперсия в явном виде не может быть использована для количественной характеристики рассеяния результатов, поскольку ее размерность не совпадает с размерностью результата анализа. Для характеристики рассеяния используют стандартное отклонение:

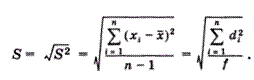
Эту величину называют также средним квадратичным (или квадратическим) отклонением или средней квадратичной погрешностью отдельного результата. Погрешность средней квадратичной погрешности может быть рассчитана по формуле

I

Таким образом, при обработке результатов анализа обычно находят выборочное среднее 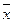, а не генеральное μ, выборочную дисперсию S² и выборочное стандартное отклонение S, а не σ² и σ, характеризующие генеральную совокупность. Тем не менее, результаты случайной выборки позволяют оценить параметры генеральной совокупности.

Для оценки воспроизводимости вычисляют выборочную дисперсию среднего значения:

С практической точки зрения, выражение для расчета дисперсии принимает вид:

и стандартное отклонение может быть рассчитано по формуле:

Пример. Рассчитаем среднее значение, дисперсию и стандартное отклонение среднего результата (при определении свинца Рb в сплаве (%): 14,50; 14,43; 14,54; 14,45; 14,44; 14,52; 14,58; 14,40; 14,49.

Принимая А = 14,50, получаем:

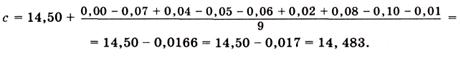
В соответствии с формулой 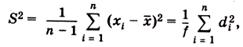дисперсия будет равна:

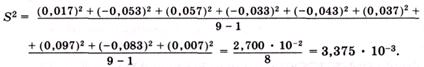
По уравнению

величина S² составляет:

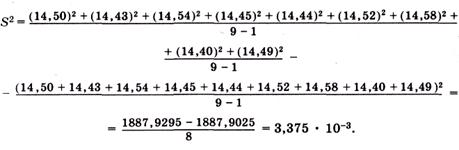
Это полностью совпадает с результатом предыдущего расчета и не требу­ется находить разность (x_i - 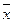), прежде чем взять соответствующий квадрат.

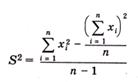
При использовании соотношения

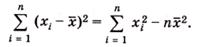
значение S² существенно зависит от округления среднего арифметического:

Приведенные результаты показывают, что истинное значение дисперсии в этом случае получается только при использовании среднего арифметического, имеющего не менее 6 цифр после запятой. Стандартное отклонение (квадратичную погрешность) рассчитываем по формуле

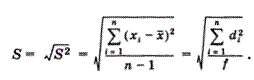
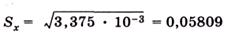
и находим стандартное отклонение среднего результата:

Дата добавления: 2014-01-11