Основная часть – до 170 мин

ЛЕКЦИЯ № 2

ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

Кафедра ЭФ-2 «Экономические информационные системы»

УТВЕРЖДАЮ

Заведующий кафедрой ЭФ-2

_________________ Лагунова А.Д.

«____»_____________2012г.

Для студентов факультета ЭФ

специальности 080801

к.т.н. Зуев А.С., к.т.н., проф. Дмитриев Я.В.

по дисциплине 5217 «Эконометрика»

ТЕМА «Характеристики случайных величин»

Обсуждена на заседании кафедры

(предметно-методической секции)

«15»мая 2012 г.

Протокол № 11

МГУПИ – 2012г.

Тема лекции:	Характеристики случайных величин
Время: 2 часа (90 мин.)
Литература (основная и дополнительная):
См. список рекомендованной литературы
ПЛАН ЛЕКЦИИ:
Введение – до 5 мин.
Основная часть (учебные вопросы) – до 80 мин.
1-й учебный вопрос	Основные понятия случайной величины.
	30 мин.
2-й учебный вопрос	Построение гистограммы.
	20 мин.
3-й учебный вопрос	Законы распределения. Биноминальный закон.
	30 мин.
Заключение – до 5 мин.
ТЕКСТ ЛЕКЦИИ
Введение – до 5 мин.

Случайные величины, их характерные особенности. Дифференциальный и интегральный закон распределения случайной величины, их построение и использование. Числовые характеристики случайных величин. Начальные и центральные моменты. Математическое ожидание, дисперсия, среднеквадратическое и среднелинейное отклонение. Определение вероятности попадания значений случайной величины в заданный интервал с помощью дифференциального и интегрального закона распределения. Эмпирические и теоретические законы распределения случайных величин. Критерий согласия Пирсона при оценке соответствия эмпирического закона априори заданному теоретическому закону распределения случайной величины.

1-й учебный вопрос

Основные понятия случайной величины

Случайная величина характеризуется тем, что в процессе опытов, осуществляемых в одинаковых условиях, находятся значения, отличающиеся друг от друга. В отличие от случайной величины неслучайная величина характеризуется тем, что в процессе опытов, осуществляемых в одинаковых условиях, получается одно и то же значение.

Любая случайная величина характеризуется, во-первых, законами распределения, во-вторых, числовыми характеристиками. Закон распределения случайной величины может быть дифференциальным и интегральным. Эти законы характеризуются тем, что они имеют графическое изображение. Числовые характеристики характеризуются количественными оценками. Они могут быть найдены на основе законов распределения и на основе исходного ряда значений случайной величины.

Для того, чтобы найти дифференциальный и интегральный закон распределения случайной величины, необходимо предварительно определить гистограмму, полигону и кумуляту, которые также как и законы распределения имеют графическое изображение.

Случайная величина имеет различные значения и их предсказать довольно сложно.

Х_n – случайная величина, nЄN.

Характеристики СВ:

- законы распределения случайной величины бывают дифференциальными и интегральными.

Для построения любого закона распределения необходимо сначала найти гистограмму, полигону и кумуляту.

Дифференциальные и интегральные значения выражаются в относительных единицах, а гистограмма, полигона, и кумулята имеют абсолютные величины.

- числовые характеристики

Могут быть найдены различным способом:

-на основе закона распределения;

- на основе ряда значений;

· Математическое ожидание

· Дисперсия

· Среднеквадратичное отклонение

· Средне линейное отклонение

· Относительный показатель – коэффициент вариации

-на основе числового ряда

· Средняя

· Мода

· Медиана

Замечание: мода и медиана может находиться и на основе закона распределения.

1. Математическое ожидание

Ищется на основе законов распределения

M(x) =

f(x) – непрерывный закон распределения

f(x_k)kϵK – дискретный закон

M(x) =

2. Дисперсия

D(x) =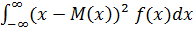

D(x) =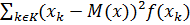

3. Среднеквадратичное отклонение

=

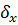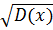
4. Среднелинейное отклонение

=

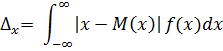
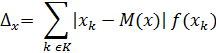
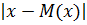5. Коэффициент вариации

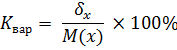
Более устойчивыми являются относительные величины, их удобно использовать для прогноза.

Дата добавления: 2014-01-13