Локальная фаза уравнений

Уравнения массо-, тепло- и импульсопередачи.

Рассмотрим перенос субстанции из фазы 1 через межфазную поверхность в фазу 2 за счет молекулярного и турбулентного механизмов. Примем, что сопротивлением переносу субстанции со стороны межфазной поверхности можно пренебречь. Это равносильно предположению об установлении равновесия на границе раздела фаз, т.е.:

m^г_i1 = m^г_i2, Т^г₁ = Т^г₂, W^г₁ = W^г₂ (2.77)

Предположим m_i1 >m_i2, тогда:

Y

2 фаза

межфазная поверхность

1 фаза

X

Рис 2.7

j^dг_iy = b_i1(m^я_i1 - m^г_i1)

(2.78)

j^dг_iy = b_i2(m^г_i2 - m^я_i2)

Разделим уравнения на b_i1 и b_i2 соответственно и их сложим:

j^dг_iy (1/b_i1 + 1/b_i2) = m^я_i1 - m^я_i2

j^dг_iy = (1/b_i1 + 1/b_i2)^-1 *(m^я_i1 - m^я_i2) = К_id * (m^я_i1 - m^я_i2) (2.79)

Здесь К_id – коэффициент массопередачи, (m^я_i1 - m^я_i2) – движущая сила массопередачи.

Уравнение (2.79) носит название уравнения массопередачи.

Химические потенциалы неидеальных (реальных) систем достаточно сложно, поэтому при анализе и расчёте процессов массопереноса обычно рассматривают изменение не химических потенциалов, а концентраций компонентов, определение которых значительно проще. Разностью между рабочими и равновесными концентрациями в одной из фаз является движущей силой массообменного процесса.

Аналогичным образом могут быть получены уравнения тепло- и импульсопередачи:

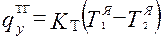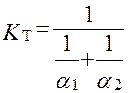, , (2.80)

если .

, , (2.81)

если .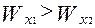

Здесь и – коэффициенты тепло- и импульсопередачи. Соотношения (2.79) – (2.81) могут быть представлены иначе:

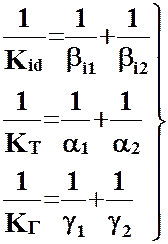(2.82)

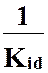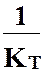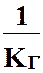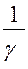Здесь , и – сопротивления массо-, тепло-, импульсопередачи (межфазные сопротивления), а , и – сопротивления массо-, тепло- и импульсоотдачи (фазовые сопротивления). Соотношения (2.82) выражают аддитивность фазовых сопротивлений. Например, если процесс теплопередачи идёт через стенку:

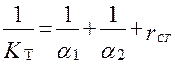, (2.83)

где – термическое сопротивление стенки.

Профили , , 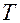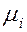в процессах переноса субстанций через границу раздела фаз, не обладающих сопротивлением, приведены на рис.2.8. Если сопротивление одной из фаз, например первой, гораздо больше второй, то последним можно пренебречь:

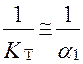, , (2.84)

Дата добавления: 2014-01-13