Решение задач по топографической карте

Содержание топографических карт и планов

Рамки карты и координатные линии. Листы топографических карт имеют три рамки: внутреннюю, минутную и внешнюю. Внутреннюю рамку образуют отрезки параллелей, ограничивающих площадь карты с севера и юга, и отрезки меридианов, ограничивающих её с запада и востока. Значения широт и долгот на линиях внутренней рамки связаны с номенклатурой карты и написаны в каждом её углу.

Между внутренней и внешней рамками помещена минутная рамка, на которой нанесены деления, соответствующие одной минуте широты (слева и справа) и долготы (наверху и внизу). Точками на рамке отмечены десятки секунд.

Система прямоугольных координат на карте представлена километровой сеткой, образованной проведенными через 1 км координатными линиями x и y. Значения x и y, выраженные в километрах, надписаны на выходах линий за внутреннюю рамку карты.

На планах масштабов 1:5000-1:500, построенных с прямоугольной разграфкой, линии параллелей и меридианов и минутная рамка отсутствуют. Линии сетки прямоугольных координат проводят здесь через 10 см. Их выходы за внутреннюю рамку надписывают в километрах (для масштабов 1:5000 и 1:2000) или в метрах (для масштабов 1:1000 и 1:500).

Условные знаки. На планах и картах все объекты местности изображают с помощью условных знаков, показывающих их местоположение и основные характеристики. При этом пользуются обязательными для всех ведомств и учреждений стандартными условными знаками, описание которых дано в официальных руководствах.

Условные знаки различают контурные, внемасштабные и линейные. Контурными условными знаками изображают объекты, форма и размеры которых могут быть переданы в масштабе данного плана или карты. К ним относятся земельные угодья (леса, сады, пашни, луга), водоёмы, а для более крупных масштабов - здания, сооружения. Внешние очертания объектов (контуры) на плане показывают точечным пунктиром или линиями определённой толщины и цвета. Внутри контура помещают условные знаки, указывающие на характер объекта.

Внемасштабными условными знаками изображают объекты, которые необходимо нанести на план, но нельзя показать в масштабе (отдельно стоящие деревья, бензоколонки, колодцы, пункты геодезической сети и др.).

Линейными условными знаками изображают объекты, длина которых выражается в масштабе плана, а ширина не выражается (линии электропередач и связи, трубопроводы, ограды, тропы).

В разных масштабах один и тот же объект может изображаться условным знаком разного типа. Для изображения здания, моста на крупномасштабном плане служат контурные условные знаки, а на карте более мелкого масштаба - внемасштабные. Железные и автомобильные дороги, городские улицы, реки могут изображаться в зависимости от масштаба линейными или контурными условными знаками. Для отражения существенных характеристик изображаемых объектов многие условные знаки сопровождаются пояснительными подписями. Так, при изображении железной дороги указывают высоту насыпи и глубину выемки, материал покрытия платформ, ширину колеи на узкоколейной дороге. При изображении шоссе – его ширину и материал покрытия; при изображении линий связи – число проводов и их назначение; при изображении лесов – породу деревьев, их среднюю высоту, толщину стволов и расстояние между ними.

Изображение рельефа на картах и планах. Рельефом местности называют характер её поверхности (например, равнинный рельеф, холмистый, горный). На картах и планах рельеф изображают с помощью горизонталей, отметок высот и условных знаков.

Горизонтали - линии сечения земной поверхности равноотстоящими уровенными поверхностями (рис. 2.5). Иными словами, горизонтали - это линии равных высот. Наглядное представление о горизонтали получим, вообразив подъём воды в море до уровня нашего участка местности, – линия уреза воды совпадёт с горизонталью. Горизонтали, подобно другим точкам местности, проецируют на уровенную поверхность и наносят на план.

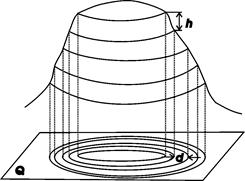
Рис. 2.5. Изображение рельефа горизонталями: h – высота сечения рельефа; d - заложение

Разность высот смежных горизонталей, равная расстоянию между соседними секущими поверхностями, называется высотой сечения рельефа. Высоты горизонталей, показываемых на плане, всегда кратны высоте сечения рельефа. Принятое на плане значение высоты сечения подписывают у нижней рамки плана. Чем меньше высота сечения рельефа, тем детальнее и точнее изображается рельеф. В зависимости от масштаба плана и характера рельефа применяют следующие высоты сечения рельефа (табл. 2.3).

Таблица 2.3

Высоты сечения рельефа, м

Характер	Масштаб
рельефа	1:500, 1:1000	1:2000	1:5000	1:10000
Равнинный Всхолмлённый Пересечённый Горный	0,5 0,5 0,5	0,5

Расстояние между соседними горизонталями в плане (горизонтальное проложение) называется заложением. Минимальным в данном месте является заложение, перпендикулярное к горизонталям, – заложение ската. Чем меньше заложение ската, тем круче скат.

Направление ската на плане указывают с помощью бергштрихов - коротких штрихов, направленных в сторону спуска, которые рисуют у некоторых горизонталей в характерных местах рельефа. На отдельных горизонталях в их разрывах пишут их высоту так, чтобы верх цифр указывал в сторону подъёма.

Для удобства чтения плана горизонтали с круглыми значениями высот делают утолщёнными, а для отражения деталей рельефа используют полугоризонтали – штриховые линии, соответствующие половине высоты сечения рельефа, а также вспомогательные горизонтали с короткими штрихами, проводимые на произвольной высоте.

Изображение рельефа горизонталями дополняется вписыванием на план отметок высот около характерных точек рельефа и специальными условными знаками, изображающими элементы рельефа, которые не удаётся описать с помощью горизонталей: обрывы, скалы, овраги и т. п.

Основными формами рельефа являются гора, котловина, хребет, лощина и седловина. Горизонталями эти формы изображаются следующим образом. (Рис. 2.6.).

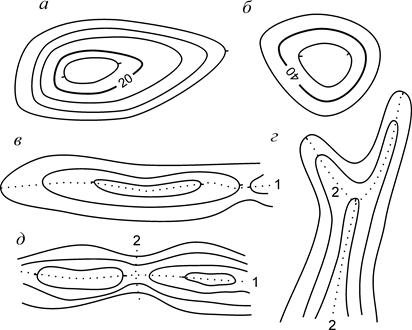
Рис. 2.6. Основные формы рельефа: а – гора; б – котловина; в – хребет; г – лощина; д – седловина; 1 – водораздельная линия; 2 – водосливная линия

Гора (возвышенность, холм, курган, сопка) изображается замкнутыми горизонталями с бергштрихами, обращёнными наружу (рис. 2.6, а). Основными характерными точками этой формы рельефа являются вершина горы и точки у её подошвы.

Котловина (впадина) тоже изображается замкнутыми горизонталями, но с бергштрихами, обращёнными внутрь (рис. 2.6, б). Основными характерными точками этой формы рельефа являются точки на её дне и у бровки.

Хребет - вытянутая в одном направлении возвышенность. Изображается огибающими гребень хребта и идущими по его скатам вытянутыми горизонталями (рис. 2.6, в). Бергштрихи, как и у горы, обращены наружу. Характерной линией хребта является проходящая вдоль его гребня водораздельная линия.

Лощина (долина, ущелье, овраг, балка) – вытянутое в одном направлении углубление. Изображается тоже вытянутыми, описывающими её форму горизонталями с бергшрихами, обращёнными внутрь (рис. 2.6, г). Характерной линией лощины является водосливная линия (тальвег) - линия, по которой сбегает вода.

Седловина – пониженная часть местности между двумя возвышенностями (рис. 2.6, д). В горах седловины называют перевалами. Через седловину и примыкающие к ней возвышенности проходит водораздельная линия. По обе стороны от водораздела к седловине примыкают лощины со своими водосливными линиями. Таким образом, седловина – это место пересечения водораздельной и водосливной линий.

Измерение расстояний на картах и планах. Для измерения расстояния между двумя точками на карте его берут на циркуль-измеритель и переносят на помещённый под южной рамкой карты линейный масштаб, где значение расстояния отсчитывают в метрах.

Более точно расстояние между заданными точками измеряют выверенной линейкой с миллиметровыми делениями. Отсчёт по линейке выражают в сантиметрах, фиксируя десятые и сотые доли сантиметра. Умножив результат измерения на число метров, указанное в именованном масштабе карты, получают расстояние в метрах.

Ещё точнее измерения выполняются с применением поперечного масштаба (рис. 2.7).

Рис. 2.7. Поперечный масштаб

На металлической линеечке через m интервалов выгравированы параллельные линии – горизонтали (обычно m = 10). К ним восставлены перпендикуляры – вертикали, расстояние между которыми называют основанием масштаба d (обычно d = 2 см). Крайнее левое основание разделено на n частей и через полученные точки проведено n наклонных линий – трансверсалей (обычно n =10 или 5). Длины отрезков, параллельных основанию, на поперечном масштабе равны: между соседними вертикалями – d, между соседними трансверсалями – d/ n. Длины отрезков между вертикалью и исходящей из той же точки трансверсалью изменяются в пределах от 0 до d/ n. Наименьшее деление поперечного масштаба, определяющее его точность, равно d/ (mn).

Для удобства пользования поперечным масштабом деления основания и горизонтали оцифровывают в соответствии с масштабом плана.

Для измерения расстояния берут его в раствор циркуля-измерителя. Правую его ножку ставят на одну из вертикалей поперечного масштаба, а левую – на одну из трансверсалей, но так, чтобы обе ножки оказались на одной и той же горизонтали. Измеренное расстояние равно сумме расстояний, соответствующих числу охваченных раствором циркуля целых оснований, десятых долей основания и сотых, оцениваемых по положению ножки циркуля на трансверсали. На рисунке отрезок ab имеет длину 20+3+0,7=23,7 м. Длина отрезка cd равна 30+5+0,45=35,45 м. Из второго примера видно, что длину отрезка удаётся измерить с точностью половины наименьшего деления (в данном случае 0,05 м).

Для измерения длин извилистых линий служит специальный прибор - курвиметр, снабжённый колёсиком, которое прокатывают вдоль измеряемой линии. Вращение передаётся на стрелку циферблата, по которому прочитывают измеренное расстояние.

Определение по карте координат. Для определения координат показанных на карте объектов служат рамки карты и километровая сетка.

Географические координаты точек определяют, опираясь на минутную рамку карты. На западной и восточной рамках находят одинаковые значения минут, ближайшие к широте определяемой точки с юга, и прочерчивают соединяющую их линию (рис. 2.8.).

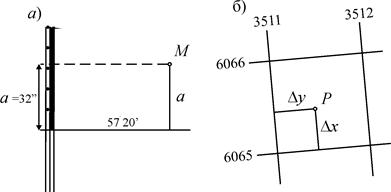
Рис. 2.8. Определение координат точек по карте:

а – географических; б - прямоугольных

На рис. 2.8, а показан отрезок такой линии со значением широты на ней 57°20¢. Взяв на циркуль-измеритель расстояние а от определяемой точки M до проведенной линии, откладывают его на рамке карты от деления 57°20¢ и, пользуясь десятисекундными делениями рамки, соображают число секунд. На рисунке число секунд равно 32", следовательно, широта точки M равна 57°20¢32".

Для определения долготы точки на северной и южной рамках карты находят одинаковые значения минут долготы и прочерчивают вертикальную линию, которая должна пройти западнее (левее) точки. Расстояние от точки до линии переносят измерителем на северную или южную рамку и считают, как и при определении широты, число секунд. Градусы и минуты, соответствующие прочерченной линии, и сосчитанные секунды дадут значение долготы.

Прямоугольные координаты точек определяют, пользуясь имеющейся на карте километровой сеткой, линии которой параллельны координатным осям x и y и проведены через 1 км. Заметив, в котором квадрате километровой сетки расположена определяемая точка, читают на выходах километровых линий за рамку значения координат: x ю- для линии, ограничивающей квадрат с юга, и y з-для линии, ограничивающей его с запада. Измерением расстояний от определяемой точки P (рис. 2.8, б) до южной и западной границ квадрата определяют приращения координат – отрезки D x и D y. Сложив соответствующие координаты и их приращения, выраженные в метрах, находят координаты точки:

xP = x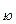+ D x; yP = y+ D y.

В нашем примере xP = 6065000 + D x; yP = 3511000 + D y.

Определение углов ориентирования. Дирекционный угол направления отрезка на карте измеряют транспортиром как угол, отсчитываемый по направлению часовой стрелки от северного направления линии километровой сетки до направления отрезка. При необходимости перед измерением отрезок удлиняют карандашом до пересечения с линией сетки. Более точным является другой способ: определяют прямоугольные координаты x 1, y 1, x 2, y 2конечных точек отрезка и вычисляют дирекционный угол по формулам (1.8) - (1.9).

Для определения азимута направления сначала измеряют его дирекционный угол a. Затем устанавливают сближение меридианов g, значение которого подписано под южной рамкой карты и показано на помещённой там же схеме. Зная дирекционный угол и сближение меридианов, азимут вычисляют по формуле (1.6).

Можно азимут измерить и непосредственно. Через одноименные значения минут долготы проводят вертикальную линию - меридиан. Угол между ним и направлением отрезка и есть азимут A.

Под южной рамкой карты и на схеме указано также склонение магнитной стрелки d, позволяющее вычислить магнитный азимут направления по формуле (1.7).

Определение высот точек по карте. Высота точки, лежащей на горизонтали, равна высоте горизонтали. Высоты отдельных горизонталей подписаны в их разрыве. Высоты других горизонталей легко сообразить, зная высоту сечения рельефа, а также высоты подписанных горизонталей и высоты тех характерных точек рельефа, у которых подписаны их отметки. При этом учитывают, что высоты горизонталей кратны высоте сечения1000 + (y.

Определение углов ориентирования. Дирекционный угол направления отрезка на карте измеряют транспортиром как угол, отсчитываемый по направлению часовой стрелки от северного направ л ения линии километровой сетки до направления отрезка. При необходя по формуле

,

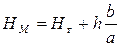где H _г - высота меньшей горизонтали, h – высота сечения рельефа, а отрезки a и b – заложение ската и расстояние от точки до горизонтали, измеряемые по карте линеечкой.

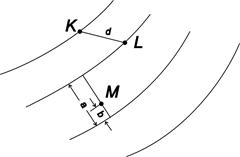
Рис. 2.9. Определение высоты точки и уклона линии

Построение профиля. Для построения профиля по линии, проведенной на карте, определяют высоты точек в местах её пересечения с горизонталями, водораздельными и водосливными линиями. Измеряют горизонтальные расстояния до них от начальной точки линии. При построении профиля по горизонтальной оси откладывают расстояния, а по вертикальной - высоты. Для наглядности вертикальный масштаб принимают крупнее горизонтального (в 10, а то и в 50 раз).

Определение уклонов и углов наклона. Отрезки линий на земной поверхности обычно имеют какой-то наклон, отчего начало и конец отрезка находятся на разных высотах. Разность их высот – превышение, а проекция отрезка на горизонтальную плоскость – его горизонтальное проложение.

Уклоном i линии называется отношение превышения h к горизонтальному проложению d:

i = h / d. (2.1)

Для определения по карте уклона линии на участке KL между двумя горизонталями (рис. 2.9) измеряют его горизонтальное проложение – заложение d. Поскольку концы отрезка лежат на смежных горизонталях, превышение h между ними равно высоте сечения рельефа, подписанному под южной рамкой карты. Воспользовавшись формулой (2.1), вычисляют улон, который принято выражать в тысячных. Если, например, h = 1 м, d = 48 м, то уклон равен i = 1 м / 48 м = 0,021 = 21‰.

С другой стороны, отношение превышения h к горизонтальному проложению d равно тангенсу угла n наклона линии. Поэтому

i = tg n,

что позволяет, вычислив уклон определить по нему угол наклона. Но при пользовании картой углы наклона определяют с помощью графика заложений (рис. 2.10), располагаемого под южной рамкой карты.

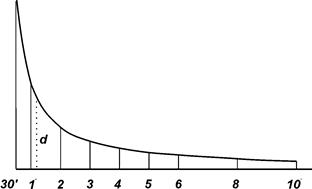
Рис. 2.10. График заложений

По горизонтальной оси графика отложены углы наклона, а по вертикальной - соответствующие этим углам заложения d, выраженные в масштабе карты и рассчитанные по формуле

d = h /M tg n,

где h - высота сечения рельефа, а M – знаменатель масштаба карты.

Для определения угла наклона расположенного между горизонталями отрезка длиною d, берут его в раствор циркуля и на графике заложений находят такой угол, над которым ордината равна раствору циркуля d. На рис. 2.10 – это угол n = 1,2°.

При необходимости многократного определения уклонов пользуются графиком уклонов, построенному аналогично графику заложений, но с отложением по горизонтальной оси не углов наклона, а уклонов.

Проведение линии с заданным предельным уклоном. Необходимость решения такой задачи возникает, например, при выборе трассы для будущей дороги. Вычисляют соответствующее заданному предельному уклону i пред заложение, выраженное в масштабе карты

d = h /M i пред.

Чтобы уклон линии не превосходил i пред, ни одно заложение на ней не должно быть меньше, чем рассчитанное d. Если расстояние между горизонталями больше рассчитанного, направление линии можно выбирать произвольно. В противном случае в раствор циркуля берут отрезок, равный d, и строят ломаную линию, умещая между горизонталями рассчитанное предельное заложение (рис. 2.11).

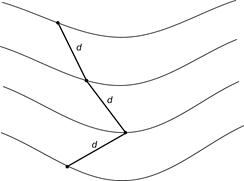
Рис. 2.11. Построение линии с заданным уклоном

Определение водосборной площади (бассейна). Водосборной называют площадь, с которой дождевые и талые воды поступают в данное русло. Определение водосборной площади необходимо, например, при проектировании дороги для расчёта отверстия моста или трубы.

Для определения границ водосборной площади на карте проводят водораздельные линии, а затем от проектируемого сооружения к водораздельным линиям проводят линии наибольшего ската, перпендикулярные горизонталям.

Например, водосборная площадь, для точки Р, где предстоит строительство трубы, (рис. 2.12), ограничена штриховой линией, образованной водораздельной и двумя линиями наибольшего ската.

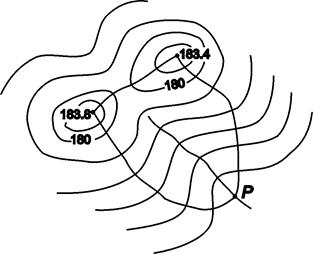
Рис. 2.12. Водосборная площадь

Дата добавления: 2014-01-13