Интегральная форма закона сохранения массы

Закон сохранения массы

ЗАКОНЫ СОХРАНЕНИЯ

При анализе технологических процессов и расчете аппаратов используются законы сохранения массы, импульса и энергии. Следует помнить, что эти фундаментальные законы сформулированы на основе многочисленного экспериментального материала и не предполагают какого-либо теоретического обоснования. Законы сохранения могут записываться применительно как ко всей системе или ее частям (интегральная форма), так и к отдельным точкам пространства (локальная форма), использоваться для среды в целом или отдельных компонентов.

Суть закона сохранения массы заключается в том, что масса не может исчезать, либо возникать, т.е. суммарное количество массы в закрытой системе неизменно (закрытая не обменивается массой с окружающей средой), следовательно, DМ = 0 или dM/dt = 0. Рассмотрим закон сохранения массы для открытых систем.

(материальный баланс)

Изменение массы в некотором фиксированном объеме V вызывается разностью прихода и отвода из выделенного объема.

(18)

где Dr - изменение плотности.

При описании непрерывных процессов, удобнее пользоваться понятием массового расхода G, который является количеством массы, прошедшим за единицу времени. Отнесем величины, входящие в уравнение (18), к бесконечно малому промежутку времени dt

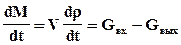(19)

Если плотность вещества не меняется (среда несжимаемая), или процесс протекает в стационарных условиях, то материальный баланс упрощается

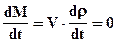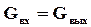® (20)

Можно записать уравнение материального баланса для каждого компонента

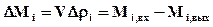(21)

Данное уравнение не является универсальным и справедливо лишь при отсутствии химических реакций в системе, т.к. в последнем случае одни компоненты могут переходить в другие. В общем случае уравнение материального баланса для каждого компонента будет иметь вид

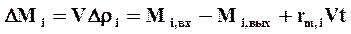(22)

где r_m,i - масса компонента i, образующаяся в единице объема за единицу времени (источник массы). Просуммировав уравнения (22) по всем компонентам мы должны получить уравнение (18) для всей массы в целом. Отсюда вытекает естественное условие на источники массы отдельных компонентов (отрицательные источники массы иногда называют стоками)

(23)

Можно переписать уравнение (22) в терминах расходов

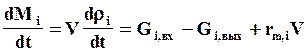(24)

Дата добавления: 2014-01-13