Условия однозначности

Исчерпывающее описание процессов переноса

Дифференциальные уравнения второго порядка в частных производных, полученные на основе уравнений переноса и законов сохранения массы, импульса и энергии или их частные случаи, а также условия однозначности к ним составляют исчерпывающее математическое описание процессов переноса (без учета переноса тепла посредством излучения). Оно, в принципе, позволяет решить как прямую задачу поверочного расчета любого аппарата, т.е. зная конструкцию и размеры аппарата, находить поля скоростей, давлений, температур и концентраций в нем; так и обратную задачу проектного расчета - определить конструкцию и размеры аппарата по требуемым значениям перечисленных выше величин на входе и выходе из него. Проблема заключается лишь в математической сложности решения этих задач.

Общее решение дифференциального уравнения описывает целый класс процессов. Для получения частного решения, соответствующего конкретным условиям проведения процесса, необходимо задание условий однозначности. Они включают:

1) геометрическую форму и размеры системы;

2) физические свойства участвующих в процессе сред;

3) начальные условия, характеризующие состояние системы в начальный момент времени (для нестационарных процессов);

4) граничные условия, характеризующие поведение системы на ее границах, либо взаимодействие с окружающей средой.

Рассмотрим математическую формулировку условий однозначности.

1) Форма и размеры системы (рабочая зона аппарата) задаются одной или несколькими поверхностями, ее ограничивающими. Так как размеры аппарата во времени не меняются, то типичные геометрические условия имеют вид Ф(х,y,z)=0. Например, поверхность вертикального цилиндра радиуса R задается уравнением Ф(х,y,z)=х²+y² - R²= 0.

2) Физические свойства среды характеризуются плотностью и коэффициентами переноса. Если правомерно допущение о постоянстве их значений, то они задаются числами. Однако, в общем случае плотность и коэффициенты молекулярного переноса зависят от температуры и соотношения концентраций компонентов, что требует задания таких зависимостей r(Т, с_i), n(Т, с_i), D(Т, с_i), а(Т, с_i). Еще сложнее дело обстоит с коэффициентами турбулентного переноса, т.к. они к тому же зависят от режима движения и пространственных координат n_т(Т, с_i, [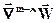], х, y, z), D_т(Т, с_i, [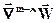], х, y, z), а_т(Т, с_i, [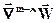], х, y, z). Единственным упрощением является близость значений этих коэффициентов в одинаковых условиях n_т~D_т~а_т.

3) Начальные условия предполагают задание значений искомых переменных в начальный момент времени в области пространства, ограниченной поверхностью Ф(х,y,z)=0, т.е., Т = Т(х,y,z,0), Р=Р(x, y, z, 0), сi= сi(х,y,z,0), i=1,n.

4) Граничные условия предполагают задание значений давлений, скоростей, температур и концентраций, либо значений потоков массы, импульса и тепла или условий, накладываемых на них на границах системы, т.е. на поверхности

Ф(х,y,z)=0: 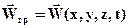, Т_гр = Т(х,y,z,t), с_iгр=с_i(х,y,z,t),

P_гр =P(x,y,z,t) i=1,n.

либо 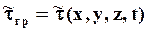, , 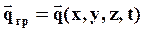, i = 1,n, (х,y,zÎФ).

Поля скорости, давления, температуры и концентраций,

Дата добавления: 2014-01-13