Розгалужені алгоритми

У випадках, коли перетворення інформації може здійснюватись за різними схемами, залежно від властивостей вхідних даних або проміжних результатів, використовуються розгалужені алгоритми. В таких алгоритмах передбачаються всі можливі варіанти обробки інформації, кожний з яких розробляється як окрема гілка алгоритму, а вибір однієї з них для виконання здійснюється за допомогою перевірки деякої умови, що відображає властивості інформації, яка використовується у процесі перетворення.

Для представлення таких алгоритмів використовуються алгоритмічні конструкції вибору (розгалуження).

Повне галуження — це розгалуження, у якому дії визначені і у разі виконання, і у разі невиконання заданої умови. Графічне представленням такої структури у блок-схемах має наступний вид:

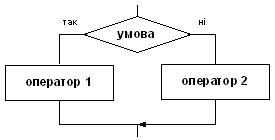
Неповне галуження — це розгалуження, в якому дії визначені тільки у разі виконання (або у разі невиконання) умови, тобто, одна із гілок взагалі не передбачає ніяких дій. Графічне представленням таких структур у блок-схемах:

Наприклад, обчислити max(x, y), x ¹ y.

Блок-схема алгоритму:

Залежно від того, на скільки гілок розгалужується алгоритм, він може бути простим або складним. Для простого розгалуженого процесу перевіряється одна умова, для складного — дві чи більше умов, кожна з яких відокремлює одну гілку. Умова формулюється таким чином, щоб відповідь перевірки була «так» чи «ні». Наприклад,

а)

б)

Складне розгалуження відбувається послідовно, з відокремленням гілок за схемою, представленою на рис. 9 а.

Збільшення кількості умов робить алгоритм більш заплутаним, він втрачає наочність, перевірити його правильність досить складно. У таких випадках необхідно перехід до будь-якої гілки розгалуженого алгоритму пов’язати з деякою змінною, кожне значення якої відповідатиме одній із гілок розгалуження, тобто одному з варіантів обробки інформації. Це можуть бути не тільки окремі значення, а й проміжки значень, до яких належатиме конкретне значення змінної. Тоді всі логічні блоки алгоритму об’єднуються в один блок аналізу цієї змінної, який матиме не два виходи, а стільки, скільки існує варіантів обробки. Таке розгалуження називають багатоваріантним.

Нехай k - змінна вибору варіантів, яка може приймати значення а ₁, а ₂,..., а _n, і існують варіанти обробки інформації, відповідні деяким переліченим значенням змінної чи їх сукупностям. Обов’язково необхідно передбачити варіант обробки, коли значення змінної не належить до перелічених значень. Тоді розгалужений алгоритм матиме вигляд, представленою на рис. 9 б:

а)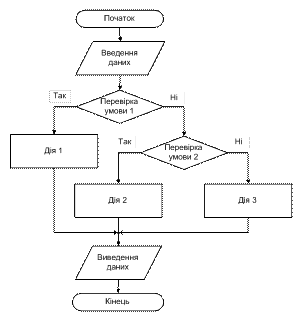

б)

Рис. 9. Блок-схеми розгалужених алгоритмів

Дата добавления: 2014-01-13