Показатели вариации признака

Под вариацией в статистике понимают такие количественные изме­нения величины исследуемого признака в пределах однородной совокуп­ности, которые обусловлены перекрещивающимся влиянием действия различных факторов.

Вариационные ряды характеризуются различными показателями.

Важной характеристикой вариационного ряда (выборки) является среднее арифметическое наблюдаемых значений признака, то есть выборочная средняя:

При оценке результатов статистического наблюдения всегда приме­няют выборочное среднее, которое в случае, когда наблюдений достаточ­но много, представляет собой хорошее приближение для генеральной средней (средней арифметической генеральной совокупности).

Однако выборочное среднее может раскрыть лишь общую тенденцию изучаемого явления и только тогда, когда она выведена из большого числа наблюдений и при наличии однородной совокупности.

Средняя величина не показывает строения совокупности, которое весьма существенно для ее познания. Она не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Одинаковые средние могут иметь совершенно разнородные совокупности.

Колеблемость отдельных наблюдаемых значений изучаемого призна­ка характеризуют показатели вариации.

Наиболее простой параметр изменения разброса значений варьирую­щего признака - размах вариации (размах колебаний).

Размах вариации R - это разность между наибольшим (x_max) инаи­меньшим (x_min) значениями вариант: R = x_max - x_min

Размах вариации улавливает только крайние отклонения, но не отражает отклонений от средней всех значений признака в вариационном ряду.

Чтобы дать обобщающую характеристику распределению отклоне­ний, вычисляют среднее линейное отклонение, которое учитывает различия всех единиц изучаемой совокупности.

Среднее линейное отклонение определяется как средняя арифметическая отклонений индивидуальных значений вариант от средней, без учета знака этих отклонений:

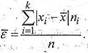
Среднее линейное отклонение как меру вариации признака применяют в статистическом анализе редко.

Более объективно отражает меру вариации показатель вариаций, называемый дисперсией.

Дисперсия представляет собой среднее арифметическое отклонений индивидуальных значений вариант от средней, возведенных в квадрат:

Чем больше дисперсия, тем больше разброс вариант относительно средней.

Средним квадратическим отклонением называют корень квад­ратный из дисперсии.

Среднее квадратическое отклонение всегда имеет ту же размерность, что и случайная величина (изучаемый признак).

Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает всю изучаемую совокупность (выборку).

Для характеристики меры вариаций изучаемого признака в относи­тельных величинах вычисляют относительные показатели вариации. Они позволяют сравнивать характер рассеивания в вариационных рядах различной размерности с разными уровнями.

Коэффициент оспилляции определяется по формуле:

Коэффициент оспилляции отражает относительную Колеблемость крайних значений признака вокруг средней.

Относительное линейное отклонение вычисляется по формуле:

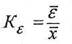
Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины.

Коэффициент вариации определяется по формуле:

Учитывая, что среднее квадратическое отклонение дает обобщающую характеристику колеблемости всех вариант вариационного ряда, коэффици­ент вариации является наиболее распространенным показателем вариации, используемым для оценки типичности средних величин. При этом исходят из того, что если К_σ > 0,4, то это говорит о большой колеблемости значе­ний признака в изучаемой совокупности.

Относительные показатели вариации часто измеряются в процентах.

Дополнительно к приведенным выше показателям отметим следую­щие показателей вариации:

децильные отношения:

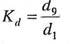
квартильные отношения:

Дециль – вариант ранжированного ряда, отсекающий десятую часть совокупности.

Квартили – значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q₁; 25% единиц совокупности будут заключены между Q₁ и Q₂; 25% - между Q₂ и Q_3/

Формулы расчета показателей вариации сведены в таблице 1.7 и таблице 1.8.

Таблица 1.7.

Формулы расчета показателей вариации

№ п/п	Наименование показателя	Формулы расчета
для несгруппированных данных	для сгруппированных данных
1.	Размах колебаний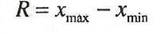
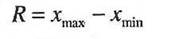
2.	Среднее линейное отклонение
3.	Дисперсия
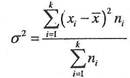
4.	Среднее квадратическое отклонение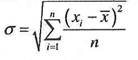

Таблица 1.8.

Относительные показатели вариации

№	Наименование показателя	Формулы расчета
1.	Коэффициент осцилляции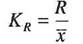
2.	Относительное линейное отклонение
3.	Коэффициент вариации
4.	Относительный показатель квартильной вариации

Дата добавления: 2014-01-13