Сложная палитра современной посткультуры

Лемма.

Быстрое возведение в степень.

Стоимость

Суммарная стоимость использования языка программирования:

Ø Стоимость обучения языку;

Ø Стоимость создания программы;

Ø Стоимость трансляции программы;

Ø Стоимость выполнения программы;

Ø Стоимость сопровождения программы.

Стоимость обучения языку определяется степенью сложности языка.

Стоимость создания программы зависит от языка и системы программирования, выбранных для реализации конкретного приложения.

Стоимость трансляции программы тесно связана со стоимостью ее выполнения.

Оптимизацией называется совокупность методов, используемых транслятором для уменьшения объема и/или сокращения времени выполнения оттранслированной программы.

Стоимость выполнения программы существенна для программного обеспечения систем реального времени.

В стоимость сопровождения программы входят затраты на исправление дефектов и модификацию программы в связи с обновлением аппаратуры или расширением функциональных возможностей. Стоимость сопровождения программы зависит от удобочитаемости языка.

Чтобы вычислить степень mⁿ, где m – элемент некоторого кольца, а n – натуральное число, достаточно выполнить не более 2[log₂n] умножений.

Доказательство. В самом деле, пусть 2^k-1 n <2^k, k-1 =[log₂n]. Тогда, записывая n в двоичной системе счисления, получим

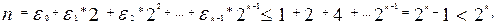
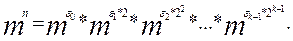
Чтобы вычислить степень 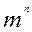, можно поступить так. Сначала вычислить степени 1, 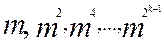. При этом достаточно выполнить k-1 умножений (возведений в квадрат). Затем некоторые из них следует перемножить. Их не более k-1. Итак, для вычисления степени потребуется не более 2(k-1) = 2[log₂n] умножений.

Рассмотрим задачу отыскания целочисленного решения уравнения вида

ax - my=1 (1)

где (а,m)=1, a>0,m>0.

Для решения этой задачи число a=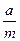 обращают в конечную цепную дробь при помощи алгоритма Евклида:

Цепная дробь имеет вид:, а последовательности {P_n} и {Q_n} числителей и знаменателей подходящих дробей к цепной дроби определяются рекуррентно:

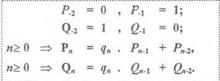
Их вычисления удобно выполнять в виде таблицы:

n	-2 -1	0 1 2... k-1 k
qn		q0 q1 q2 ... qk-1 qk
Pn	0 1	P0 P1 P2... Pk-1 Pk
Qn	1 0	Q0 Q1 Q2 ... Qk-1 Qk

Но известно, что

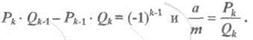
Таким образом,

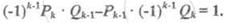
А так как (a,m)=1,то P_k=a, Q_k= m.Поэтому

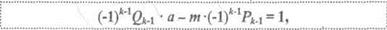
другими словами, пара <x,y>, где

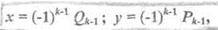
является целочисленным решением уравнения (1).

Решения сравнения первой степени.

Чтобы найти решение сравнения a*xº1(mod m), где (a,m)=1, обычно используют алгоритм Эвклида, и тогда xº(1)^k-1 Q_k-1(mod m), где Q_{k-1 –} знаменатель предпоследней проходящей дроби разложения 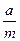в цепную дробь, теорема Ферма – Эйлера, которая утверждает, что если (a,m)=1, то

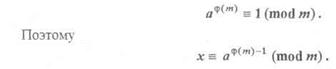
Пример. Решить сравнение.

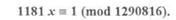
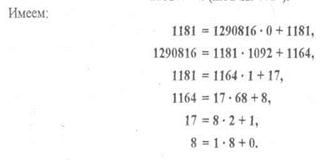
и
qn
Рn
Qn

Криптосистема без передачи ключей,криптосистема с открытым ключом.

Криптосистема без передачи ключей.

Пусть абоненты А, В, С,... условились организовать секрет­ную переписку между собой. Для этой цели они выбирают достаточно боль­шое простое число p и такое, что р -1 хорошо разлагается на не очень большие простые множители. Если среди множителей такого числа кратных нет, то число р - 1 называют евклидовым. Каждый из абонентов независимо один от другого выбирает случайное число, натуральное, взаимно простое с числом р- 1: А, В, С,... - абоненты; а, Ь, с,... - выбранные ими случайные числа. Далее, абонент А находит число a из условия:

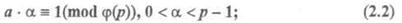
абонент В находит число b из условия:

(2.3)

a, а - секретные ключи абонента А; b, b — секретные ключи абонента В и т.д.

Пусть абонент А решает послать сообщение m абоненту В; можно предпола­гать, что 0 < m < р- 1. Тогда он сначала зашифровывает это сообщение сво­им первым секретным ключом, находит

и отправляет абоненту В. Абонент В, в свою очередь, зашифровывает вновь это сообщение также своим первым ключом:

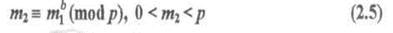
и пересылает его обратно абоненту A. Абонент А, получив обратно свое два­жды зашифрованное сообщение, шифрует его же в третий раз своим вторым ключом:

(2.6)

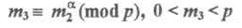
и вновь отправляет его абоненту В. Последний расшифровывает эту шифротелеграмму при помощи своего второго ключа:

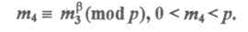
В самом деле, из сравнений (2.4), (2.5) и (2.6) имеем

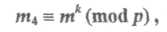
где

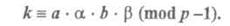
В силу (2.2) и (2.3)

Поэтому m₄= m(mod p), а так как каждое из них положительно и меньше р, то

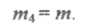
Пример. Предположим, что абоненты А и В решили установить между собой скрытую связь без передачи ключей. Они выбрали для этого простое число p = 23, далее абонент A выбирает случайным образом число а = 5, або­нент В также случайно выбирает число Ь = 7.

Затем А, решая сравнение 5 • х º 1(mod j(23)), находит х =9, анало­
гично В из сравнения 7 • х = l(mod 22) находит х = 19. Числа 5 и 9 - секрет­ные ключи абонента А, числа 7 и 19 - секретные ключи абонента В. Абонент А решает секретно передать очень важное сообщение m = 17 абоненту В. То­гда он сначала шифрует это сообщение своим первым ключом 5:

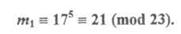
Второй абонент, получив это сообщение, шифрует его также своим первым ключом 7 и отправляет его обратно абоненту А:

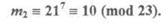
Абонент А вновь шифрует полученное сообщение своим вторым ключом 9 и отправляет новое шифрованное сообщение абоненту В:

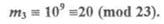
Получив это сообщение, абонент В расшифровывает его при помощи своего второго ключа 19:

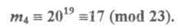
И так как 0 < 17 < 23, то m = 17

Речь по случаю вручения премии имени Адорно, учрежденной городом Франкфурт-на-Майне за 1980 г. Перевод сделан по тексту, опубликованному в: Wege aus der Moderne: Schliisseltexte der Postmoderne-Diskussion. Hrsg. von W. Welsch. Weinheim, 1988, S. 177—192.

Вниманию читателей предлагается русский перевод книги «Философский дискурс о модерне. Двенадцать лекций» («Der philosophische Diskurs der Modeme. Zwolf Vorlesungen») Ю. Хабермаса — пожалуй, одного из самых известных философов современности. Эта работа, изданная впервые в 1985 г.

Хабермас Ю. Модерн - незавершенный проект

По поводу термина – постмодерн, анти модерн

Пост история

Постпросвещение

Термин возник на рубеже 5 века как свидетельство перехода от римской культуры к раннему средневековью

Modernitat – переход к современности

-поиски нового

Поиски идеализации

-абстрактное противостояние истории

Сохранение связи с античностью

Эстетический модерн – начиная с Бодлера,Ю, середина 19 века.

Т.Адорно. «Признаки разброда суть начала подлинности модерна»

Взрыв – инвариант модерна

Современность как сейчасность В.Беньямин

Авангард – атрибут модерна

Культ нового

Коммуникативные структуры жизненным миров

Реакции на социальные модернизации

разрушение городской и природной сред обитания,

разрушение форм гуманного общежития

Проект Просвещения

Происходит дифференциация науки. Морали, искусства. Появляетсякаста экспертов

Рационализация культуры обедняет жизненный мир

Происходит резкое расслоение на элиту и плебс

Проект модерна, сформулированный в XVIII в. философами Просвещения, состоит ведь в том, чтобы неуклонно развивать объективирующие науки, универсалистские основы морали и права и автономное искусство с сохранением их своевольной природы, но одновременно и в том, чтобы высвобождать накопившиеся таким образом когнитивные потенциалы из их высших эзотерических форм и использовать их для практики, т.е. для разумной организации жизненных условий.

Дата добавления: 2014-01-13