Понятие аналого-цифрового преобразования

ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ. МИКРОПРОЦЕССОРЫ

Вопросы для самотестирования

1 Чем характеризуются последовательные регистры (регистры сдвига)? Из чего они состоят?

2 Какие логические устройства называются преобразователями кодов? Какие основные операции входят в процедуру их синтеза?

3 Укажите основные способы построения счётчиков импульсов с коэффициентом счёта, не равным 2ⁿ.

4 Охарактеризуйте параметр «импульсная помехоустойчивость» логического элемента.

5 Что характерно для таблицы состояний дешифратора двоично-десятичного кода в единичный десятичный код?

У аналого-цифровых преобразователей можно выделить пять генерализированных (наиболее общих) методовпреобразования непрерывной величины Y в код [6]. Первый из них – это преобразование « физическая величина – временной интервал Dt – код». Преобразование Y Þ Dt является аналоговым (непрерывным), а преобразование D t Þ КОД – дискретным. Геометрическая интерпретация времяимпульсного метода и структура преобразователя Dt Þ КОД приведены на рисунке 3.1.

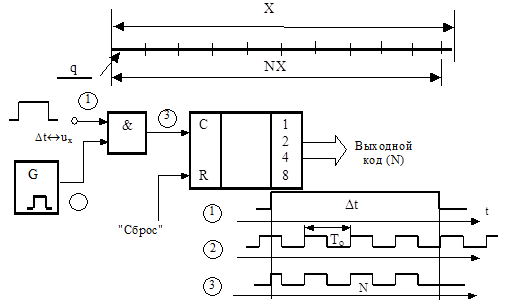
Рисунок 3.1 – Преобразователь «длительность импульса–код»

Число импульсов, подсчитанных счётчиком, определяется из выражения:

N = Dt/T_o = f₀ × Dt. (3.1)

При втором, частотно-импульсном методе, при оценке длины отрезка X, если нет отрезков единичной длины, а есть большой отрезок известной длины Aq, – то отрезок X вкладывается в отрезок Aq. Число вложений подсчитывается (рисунок 3.2).

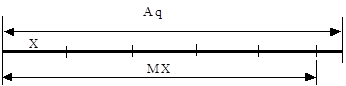
Рисунок 3.2 – Геометрическая интерпретация частотно-импульсного метода

Длина неизвестного отрезка определится следующим образом:

X = Aq/M. (3.2)

Метод характеризуется последовательным счётом повторяющейся измеряемой величины и используется, если оцениваемая величина преобразована в частоту следования импульсов: XÞYÞfÞКОД. Структура преобразования fÞКОД приведена на рисунке 3.3.

Число импульсов, подсчитанных счётчиком, определяется по формуле:

М = Dt_о/T_x = f_x × Dt_o. (3.3)

Рисунок 3.3 – Преобразователь «частота импульсов – код»

Для геометрической интерпретации третьего метода – кодоимпульсного метода – можно использовать набор отрезков, длины которых соответствуют весовым коэффициентам двоичного кода (2⁰; 2¹; 2²; 2³) и равны q, 2q, 4q, 8q (рисунок 3.4).

Метод характеризуется наличием нескольких мер, кратных кванту и относящихся как весовые коэффициенты кода; количеством мер, равным числу разрядов кода;комбинации мер по логической программе сравниваются с измеряемой величиной, приближаясь к ней.

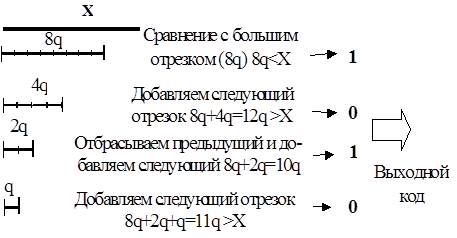
Рисунок 3.4 – Геометрическая интерпретация кодоимпульсного метода

Функциональная схема метода приведена на рисунке 3.5.

Рисунок 3.5 –Функциональная схема кодоимпульсного метода

Временные диаграммы, характеризующие работу кодоимпульсного преобразователя, приведены на рисунке 3.6 (для 4-разрядного двоичного кода). При четырёх разрядах кода потребовалось 5 тактовых импульсов (число тактов на единицу больше числа разрядов).

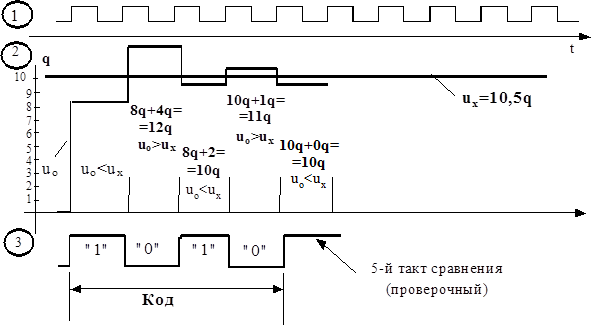
Рисунок 3.6 – Временные диаграммы кодоимпульсного преобразователя

Четвёртый метод – это метод пространственного кодирования (рисунок 3.7), который применяется при преобразовании величины X в угловое (a) или линейное (l) перемещение: X Þ a; X Þ l. Это аналоговое преобразование.

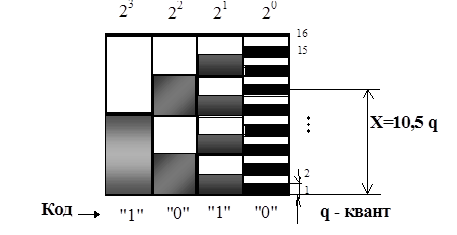
Рисунок 3.7 – Пример кодовой маски

Преобразование перемещения в код - дискретное преобразование. Метод имеет заранее заготовленные комбинации мер, кратных кванту, т. е. кодовую маску. В столбцах маски чередуются участки, соответствующие различным физическим свойствам, например: проводник-изолятор, прозрачность-непрозрачность.

Метод характеризуется считыванием состояний всех разрядов одновременно. Применяется в пространственных АЦП угловых и линейных перемещений в код.

При исследовании электрических сигналов также используется пятый метод – метод считывания (или параллельный метод). В нём напряжение постоянного тока сравнивается с рядом постоянных опорных напряжений, количество которых равно количеству квантов (рисунок 3.8).

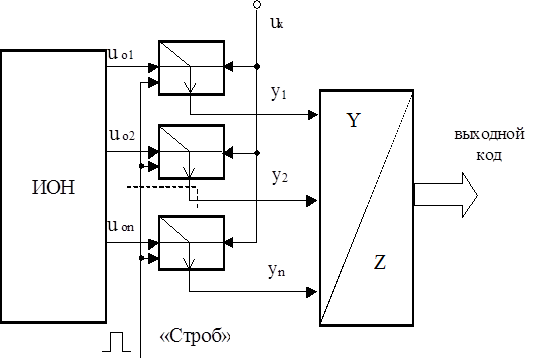
Рисунок 3.8 – Функциональная схема метода считывания

Данный метод обладает принципиально максимальным быстродействием, но и аппаратной избыточностью.

Наиболее сложным узлом всякого АЦП является его узел аналогового преобразования, в основном определяющий погрешность АЦП. Простейшим примером АЦП является времяимпульсный преобразователь с линейной развёрткой (однотактный). Он даёт приемлемую для практических случаев точность преобразования при простой схемной реализации с современной элементной базой.

Преобразование входного напряжения u_x во временной интервал t_x является аналоговым (u_x и t_x – непрерывные по значению величины). Преобразование интервала t_x в число импульсов N_x – аналого-цифровое, т. к. N_x – дискретная величина. Соотношение N_x и t_x определяется выражением N_x = f₀t_x, где f₀ – частота опорного генератора (ОГ) (частота импульсного сигнала, проходящего через временной селектор – схему И – за интервал времени t_x), рисунок 3.9.

Квант такого преобразователя равен единице младшего разряда, т. е. в единицах времени – периоду сигнала ОГ, равного 1/f₀. Максимальное значение абсолютной погрешности дискретности равно ± 0,5f₀.

Рисунок 3.9 – Времяимпульсный АЦП с линейной развёрткой

На рисунке 3.10 приведены временные диаграммы, иллюстрирующие работу АЦП (точки наблюдения 1–4). Здесь t_Ф, t_ПОД – длительность интервалов фиксации результата преобразования и подготовки к следующему; Т_{Ц ПР} – длительность цикла преобразования.

Рисунок 3.10 – Временные диаграммы однотактного АЦП

Длительность интервала t_x можно определить, зная крутизну (скорость) V линейно нарастающего участка сигнала ГПН U_ГПН: U_ГПН = Vt; u_x = Vt_x; t_x = U_x/V. Уравнение преобразования однотактного АЦП соответствует N_x = (f₀/V)u_x. Уравнение преобразования указывает, что неточность установки и нестабильность значений f₀ и u_ГНП приводят к появлению мультипликативных погрешностей. Из алгоритма работы аналогового преобразователя следует, что неточность сравнения значенийu_x и u_ГПН приводит к появлению аддитивной погрешности.

При использовании ГПН, построенного на основе интегратора на ОУ, величина u_ГПН вычисляется согласно выражению:

, (3.4)

а крутизна напряжения его сигнала определяется как V = du_ГПН / dt = -U₀t₀. И уравнение преобразования имеет вид: N_x = -(f₀t₀ / U₀)u_x. Факторами, определяющими величину суммарной погрешности АЦП, являются:

– неточность установки и нестабильность значения частоты ОГ f₀;

– неточность установки и нестабильность значений постоянной времени интегратора ГПН t₀ и опорного напряжения U₀;

– нелинейность напряжения сигнала ГПНu_ГПН;

– смещения нулевого уровня интегратора ГПН и компаратора;

– конечное значение чувствительности (определяемое шириной петли гистерезиса) компаратора.

Однотактный АЦП чувствителен к воздействию помехи нормального вида (напряжение сигнала помехи u_ПОМ и входное напряжение суммируются на входе АЦП).

Рассмотрим погрешность дискретности на примере преобразователя времяимпульсного типа. Погрешность дискретности возникает при преобразовании непрерывной величины t_Xв дискретную N _XT₀. Совокупность значений погрешностидискретности – функция случайной величины – значений величины u_x. Значенияu_xв пределах каждого дискрета T _oравновероятны – т. е. закон распределения погрешности дискретности – это закон равномерной плотности. Плотность распределения абсолютной погрешности дискретности D_д показана на рисунке 3.11. Так как график симметричен относительно оси ординат, то матожидание (среднее значение) погрешности дискретности М(D_д) = 0.

Рисунок 3.11 – Плотность распределения абсолютной погрешности дискретности

Максимальное значение абсолютной погрешности дискретности может быть равно (импульс ОГ входит или не входит в интервал t_X). Тогда

. (3.5)

Абсолютная погрешность дискретности – это разность между входным напряжением и выходным значением преобразователя:

D_д = + u_o/2N₁, (3.6)

это полкванта в размерности напряжения. Дисперсия погрешности соответствует

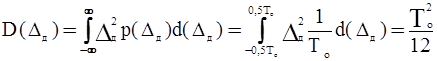. (3.7)

Среднеквадратичное значение (СКЗ) погрешности дискретности:

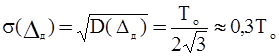, или . (3.8)

Аналогично дисперсия относительно кванта соответствует . (3.9)

Дата добавления: 2014-01-13