Лекция №9. Электронограммы пластинчатых текстур

Электронограммы пластинчатых текстур.

Если кристаллики, составляющие поликристаллическую пленку, ориентированы так, что какая-либо кристаллографическая плоскость у всех кристалликов параллельна плоской поверхности пленки, а вокруг оси, перпендикулярной этой поверхности, повернуты произвольно, то возникает так называемая пластинчатая текстура. Общим для кристалликов является направление указанной нормали, которое и является осью текстуры. Это чаще всего встречающаяся текстура среди исследуемых электронографическим методом.

Тонкие пленки, приготовленные конденсацией из паров, кристаллизацией из раствора на подложке, электролитическим осаждением, часто обладают такой текстурой.

Из определения пластинчатой текстуры очевидно, что узловые направления в обратной решетке каждого кристаллита параллельны оси текстуры. Вращая обратную решетке отдельного кристаллита вокруг оси текстуры, проходящей через начало координат, получим обратную решетку пластинчатой текстуры. Каждый узел, кроме узлов, лежащих на оси, превратится при этом в кольцо. Кольца эти лежат на коаксиальных цилиндрах, ось которых и есть ось текстуры (рисунок). Если, как это часто бывает, ось текстуры совпадает с осью кристаллов ортогональных решеток или кристаллы принадлежат кубической сингонии, то концентрические кольца, кроме того, лежат в плоскостях, перпендикулярных оси текстуры.

Электронограмма изображает сечение обратной решетки в масштабе С=lL. Поэтому вид электронограммы зависит от взаимной ориентации оси текстуры и пучка электронов.

Если пучок параллелен оси текстуры, электронограмма представляет систему концентрических колец, соответствующих отражениям от плоскостей, входящих в одну зону, ось которой есть ось текстуры. Поэтому индексы колец должны удовлетворять условию зональности.

В случае не очень строгой текстуры «узел» обратной решетки изображается широким сферическим поясом. Поэтому при построении сечения обратной решетки сферой Эвальда возможно пересечение таких полюсов, соответствующее отражению от плоскостей и не входящих в зону, ось которой – ось текстуры. Обычно эти кольца на электронограмме менее интенсивны, чем это вытекает из величин структурных амплитуд для данных отражений.

Если пучок электронов составляет острый угол с осью текстуры, то получается электронограмма косой текстуры.

Пусть угол между пучком и осью текстуры d. Для определенности положим, что ось текстуры совпадает с осью а₃ (или b₃ в обратной решетке). Тогда семейство концентрических окружностей, расположенных в одной плоскости, перпендикулярной оси а₃ имеет одно значение индекса H₃. Пересечение плоскости электронограммы с этими окружностями даст рефлексы, лежащие на одной прямой – слоевой линии (см. рисунок). Семейство же окружностей постоянного радиуса, лежащих вдоль одного цилиндра (каждой окружности соответствует свое значение H₃), пересекается этой плоскостью по эллипсам. Из рисунка очевидно, что

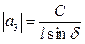
где l – расстояние между слоевыми линиями.

Угол d легко найти из той же электронограммы:

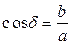
где b, а – оси эллипса.

Если угол d=90⁰, то электронограмма похожа на электронограмму несовершенного монокристалла. Однако индексы рефлексов, лежащих в одном плоском сечении, не удовлетворяют условию зональности. Кроме того, при вращении препарата вокруг оси текстуры вид электронограммы не меняется в отличие от нормальных точечных электронограмм, где поворот дает новое сечение обратной решетки.

Электронограммы от поликристаллов.

Обратная решетка совокупности беспорядочно ориентированных кристалликов показана на рисунке. Почти плоское ее сечение дает систему концентрических колец. Каждое кольцо соответствует определенному вектору обратной решетки, который здесь в отличие от случаев монокристаллов и текстур теряет все признаки своего пространственного расположения относительно других векторов, кроме длины. Таким образом, геометрия электронограммы поликристалла сводится к набору длин векторов |H|, т.е. к набору межплоскостных расстояний d_H, присущих данной решетке. Поэтому принципы индицирования электронограмм поликристаллов те же, что и при индицировании дебаеграмм.

Основным недостатком таких электронограмм является трудность их индицирования, которая усугубляется относительно невысокой точностью определения величин d_H по сравнению с рентгенодифракционными методами.

Достоинство электронограмм поликристаллов в том, что кольца, как правило, обладают меньшей угловой протяженностью, чем рефлексы точечных электронограмм; это позволяет получать несколько большую точность в измерении величин d_H. Именно поэтому такие электронограммы снимают для определения постоянной прибора (С=lL). Кроме того достоинством кольцевых электронограмм является также и то, что без вращения образца соотношение интенсивностей отражений на кольцевых электронограммах отражает величину соответствующих структурных амплитуд.

Интенсивность, приходящаяся на все кольцо электронограммы, отвечающее индексам отражения H_i равна:

Радиус кольца:

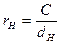
Длина кольца 2pС/d_H. Обычно измеряется не интенсивность приходящаяся на кольцо, а ее часть D. Тогда энергия приходящаяся на отрезок D есть:

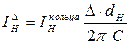
или

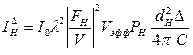
Эта формула справедлива, если частицы столь малы, что эффектами экстинкции можно пренебречь. Это в каждом конкретном случае требует проверки путем сравнения интенсивностей разных порядков отражения.

Применение медленных электронов для исследования

атомной структуры поверхности кристаллов.

С помощью дифракции медленных электронов с энергией до 1000 эВ можно изучать структуру поверхностных слоев кристаллов, толщина которых составляет один, два или несколько атомных слоев. Это дает возможность получить данные о расположении атомов на чистой поверхности тел, проводить изучение колебаний поверхностных атомов; в сочетании с Оже-спектроскопией, позволяющей проводить анализ химического состава поверхностных слоев толщиной в несколько ангстрем, изучить изменения структуры при адсорбции атомов других веществ на поверхности. В частности, возможно изучение образования двумерных зародышей на поверхности кристалла при эпитаксиальном росте, представляющее значительный интерес для понимания этого явления.

Для предотвращения адсорбции атмосферных газов на поверхности объект помещают в глубокий вакуум, а поверхность или создают непосредственно в вакууме путем раскалывания кристалла, или очищают бомбардировкой ионами инертных газов с последующим отжигом в вакууме для восстановления нарушенной бомбардировкой структуры.

Во многих случаях поверхностные слои твердого тела структурно отличаются от внутреннего объема: это либо перестроенная поверхностная грань, либо адсорбированный слой, либо перестроенный из-за адсорбции слой и т.д.

Существует пять двумерных решеток Бравэ: косоугольная, прямоугольная (примитивная или центрированная), квадратная и гексагональная. Комбинация этих ячеек Бравэ с десятью различными точечными группами дает 17 возможных двумерных пространственных групп. Сопоставлять решетку Бравэ объема и поверхности удобно введя базисные вектора трансляций `А<sub>i</sub> и `а_i (i=1,2) поверхности и объема: А_i=M_ij ^.`a_j (i,j = 1,2). Причем детерминант матрицы 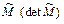есть отношение площадей сопрягающихся ячеек. Это дает удобную систему классификации структурного соответствия поверхностного слоя и объема.

а) Если 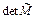целое число и все M_ij целые числа, ячейки связаны однозначно. Причем слой и поверхность объемного кристалла имеют одинаковую трансляционную симметрию.

б) Если 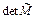рациональная дробь (или 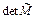- целое число, а элементы матрицы M_ij рациональные дроби) то структуры соизмеримы, но истинная поверхностная ячейка объемного кристалла больше, чем у слоя. Размер такой поверхностной ячейки определяется расстояниями на которых обе ячейки совпадают – совпадающие сетки.

в) 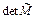- иррациональное число. Две ячейки не соизмеримы, подложка является просто плоской поверхностью, на которой адсорбируется слой с собственной двумерной структурой.

Электрон, выходя из источника, образует сферическую волну, которая рассеивается поверхностью образца. Областью, где рассеянные волны когерентны, будем считать первую зону Френеля:

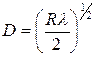
где R - расстояние от источника до поверхности.

В реальном эксперименте зона когерентного рассеяния:

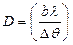
где Dq - расходимость пучка электронов, b~0,35 – критерий пространственной когерентности. Оценки показывают, что при реальной расходимости пучка ~10^-3 рад. D<1мкм. Остальные области на которые попадает пучок рассеивают некогерентно.

Особенности геометрии картин дифракции медленных электронов обусловлены, во-первых, тем, что длина волны медленных электронов по порядку величины совпадает с длинами волн рентгеновских лучей, используемых в структурном анализе; во-вторых, малая глубина проникновения электронов в кристалл даже при больших углах скольжения определяет то, что условия дифракции близки на двумерных объектах.

Условия возникновения дифракционных пучков, связывающие направление первичного и дифрагированного лучей, по-прежнему иллюстрируются с помощью построения Эвальда. Обратная решетка двумерного кристалла может быть представлена в виде стержней, закон расположения которых соответствует одной из пяти возможных плоских решеток Бравэ. Положение стержней, на сечении перпендикулярном стержням, определяется вектором ОР:

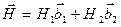
а осевые векторы

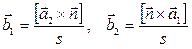
где `а_i - осевые векторы атомной сетки,

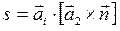
`n – единичный вектор нормальный к поверхности.

На рисунке показано построение Эвальда для дифракции на двумерной решетке. Особенно просто связать вектор рассеяния

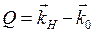
с вектором ОР 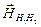при перпендикулярном падении пучка электронов на поверхность. В этом случае

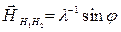
где j - угол между нормалью к поверхности и отраженным пучком, l - длина волны электронов.

При наклонном падении пучка узлу H₀₀, проходящему через начало координат, соответствует зеркально отраженный луч. В этом случае углы отражения y_H и падения y₀ связаны соотношением:

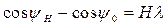
где H – вектор ОР плоской сетки.

Распределение пучков рассеянных электронов в пространстве вокруг кристалла и их интенсивность можно фиксировать с помощью перемещающегося в вакууме цилиндра Фарадея. Для визуального наблюдения дифракционной картины на флюоресцирующем экране используют метод ускорения дифрагированных электронов однородным электрическим или магнитным полем. По дифракционной картине, можно построить плоское сечение обратной решетки, параллельное поверхности рассеивающего объекта, т.е. параллельное плоскости двумерной поверхностной атомной решетки. Это позволит определить симметрию и размер двумерной элементарной ячейки поверхностной структуры кристалла. Для индицирования электронограммы в плоскости обратной решетки в соответствии с ее симметрией по правилам двумерной кристаллографии необходимо выбрать направления двух осей. Плоская группа симметрии определяется по погасаниям, закон которых в большинстве случаев можно установить после индицирования плоского сечения обратной решетки. Индицирование производят на основе базисных векторов ОР атомной сетки в объеме, параллельной поверхности. Это означает, что если верхняя атомная сетка обладает большими периодами, то стержни будут иметь дробные индексы (рисунок). Запишем структурную амплитуду для случая показанного на рисунке:

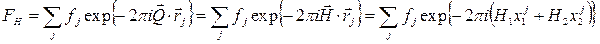
где x_i^j – координаты атомов двумерной ячейки. Эта величина разная для узлов, изображенных светлыми и темными кружками.

При образовании упорядоченной структуры на поверхности начало координат упорядоченных ячеек в разных точках поверхности может быть произвольно. Это приведет к нарушению трансляционной симметрии. Результирующая структура будет состоять из доменов с идеально периодической структурой, содержащих достаточно большое число ячеек, но возникает нарушение периодичности за счет смещения этих доменов с образованием антифазных доменных границ. Если домены достаточно велики и рассеивают некогерентно, то сложение интенсивности, рассеянной разными доменами, может приводить к тому, что симметрия дифракционной картины не соответствует симметрии ячейки. Так на подложке квадратной, может возникнуть упорядоченное расположение адсорбированных атомов с прямоугольной ячейкой. Но ячейки в разных доменах могут быть повернуты друг относительно друга на 90⁰. Суммарная же дифракционная картина будет иметь симметрию с осью четвертого порядка. Если домены рассеивают когерентно, то суммарную амплитуду можно записать в виде:

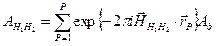
где r_p=n_i`a_i – вектор, задающий начало координат каждого из Р рассеивающих доменов; А_д – амплитуда, рассеянная одним доменом.

В принципе n_i не обязательно целая величина. Если произведение 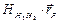кратно (m+1/2) где m –целое число, то домены рассеивают в противофазе. В этом случае происходит взаимное ослабление отраженных пучков.

Наличие ступеней на поверхности приведет к эффекту, описанному выше для дифракции быстрых электронов.

Для полного описания структуры поверхности недостаточно информации о расположении атомов в моноплоскости, необходимо определить их координаты в нескольких прилежащих к верхнему слоях и расстояния между слоями. Это можно осуществить на основе анализа эффектов трехмерной дифракции на электронах. Они приводят к наложению на стержни двумерной дифракции узлов трехмерной дифракции. Расстояние между узлами вдоль стержней обратно пропорционально среднему расстоянию между атомными слоями. Кроме того, некоторые узлы трехмерной дифракции могут и не совпадать со стержнями.

Для описания интенсивности дифрагированных пучков воспользуемся следующими простейшими представлениями. Для двумерной идеальной решетки структурная амплитуда имеет вид:

где f_j – атомная амплитуда рассеяния;

х^j_1,2 – координаты атомов поверхности в долях основных трансляций;

exp{-M_j} – фактор Дебая-Валлера.

Если увеличить энергию электронов, число атомных слоев, участвующих в рассеянии, тоже увеличится. В этом случае интенсивность, соответствующая рефлексу H₁H₂, равна:

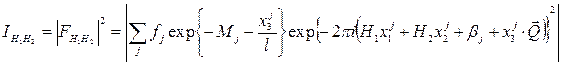
где x₃^j – нормальная к поверхности координата атома j;

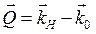- вектор рассеяния;

ехр{-x₃^j/l} – множитель, указывающий затухание первичного пучка по мере углубления его в кристалл;

l – характеристическая глубина проникновения электронов в кристалл, увеличивающаяся с ростом энергии электронов;

b_j – изменение фазы при рассеянии атомом j.

Суммирование производится по всем атомам ячейки трехмерной решетки с учетом того, что в поверхностных слоях возможны некоторые смещения атомов из положений, характерных для ячейки трехмерного идеального кристалла. В уравнении в качестве параметра содержится толщина рассеивающего слоя l, которая может быть определена по протяженности узла обратной решетки трехмерной дифракции на основе соотношения (sinpql/pq). Из экспериментально определенной ширины зеркально отраженного максимума при изменении y₀ (при постоянной энергии электронного пучка) можно оценить толщину рассеивающего слоя по формуле:

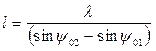
где y₀₁,y₀₂ – начальный и конечный углы падения пучка на кристалл, когда наблюдается рефлекс, соответствующий трехмерной дифракции.

Для определения расстояния между атомными слоями или величины среднеквадратичных смещений необходимо измерить зависимость интенсивности рефлекса от энергии первичного пучка I(U).

Уравнение () хотя и не опирается на последовательную физическую картину рассеяния, тем не менее во многих случаях достаточно хорошо описывает экспериментально полученную зависимость I(U).

По температурной зависимости интенсивности отражений можно найти среднеквадратичные смещения поверхностных атомов, исследуя дифракционные максимумы, соответствующие разным энергиям электронов, можно проследить зависимость величины смещений от глубины расположения атомов.

Дата добавления: 2014-01-13