За единицу измерения плоского угла в международной системе(СИ)принят радиан

НОРМИРОВАНИЕ ТОЧНОСТИ УГЛОВЫХ РАЗМЕРОВ

7.1. Система единиц на угловые размеры

Углом в плоскости называется геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины).

Двугранным углом называется геометрическая фигура в пространстве, образованная двумя полуплоскостями, исходящими из одной прямой, а так­же часть пространства, ограниченная этими полуплоскостями. Полуплос­кости называются гранями двугранного угла, а их общая прямая - ребром.

В промышленности чаще всего приходится иметь дело с двугранными углами, однако для удобства измерений требования к точности относятся к углу в плоскости, т.е. углу, получаемому пересечением двугранного угла плоскостью, перпендикулярной ребру.

Наиболее распространенными угловыми деталями в машиностроении являются конусы. Используются только круговые конусы, т.е. детали, кото­рые представляют собой поверхность вращения, образованную прямой, вращающейся относительно оси и пересекающей ее. В промышленности чаще исполь­зуются усеченные конусы, т.е. такие, которые пересечены плоскостью, параллельной основанию (окружности).

Радианом называется угол между двумя радиусами (сторонами угла), вырезающий на окружности дугу, длина которой равна радиусу:

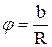, где b - длина дуги, R - радиус окружности.

Более удобной для измерений является система единиц, основанная на градусной мере, в которой для отсчета угла используются градус, ми­нута и секунда. Особенность этой системы заключается в использовании шестидесятичной системы счисления, т.е. более крупные единицы содержат 60 значений более мелкой.

Градусом (°) называется единица плоского угла, равная 1/360 час­ти окружности. Градус равен 60 угловым минутам ('), а минута - 60 уг­ловым секундам ('').

Соотношения между градусом и радианом:

360° = 2π = 6,28318530 рад; ;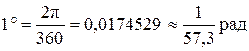

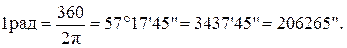
В машиностроении для удобства измерения отклонение угла от задан­ного выражают в линейной мере как изменение размера на определенной длине. Так, для указания точности угла наклона (рис.7.1) нормируются допусковые значения h, мкм, на длине L. Для пересчета линейных и уг­ловых значений надо запомнить, что на длине 206,3 мм (можно принять 200 мм) значение h, равное 1 мкм, соответствует углу в 1''. Соответс­твующий пересчет производится при других длинах и высотах с учетом указанного соотношения.

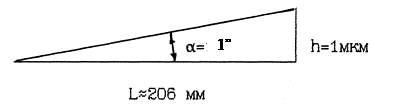
Рис. 7.1. Пересчет угловых величин в линейные

Таким образом, в машиностроении значение угла выражают либо в радианах, либо в градусах, либо размером в линейной мере на определенной длине, т.е. можно использовать три единицы для нормирования точности угловых размеров.

7.2. Нормирование требований к точности угловых размеров

1. Основные понятия

Для угловых размеров, так же как и линейных, существуют ряды нормальных углов. Однако в отношении углов это понятие используется реже, поскольку при разработке элементов деталей с угловыми размерами значе­ние угла часто получается либо расчетным путем для обеспечения определен­ных функций разрабатываемой конструкции механизма, либо определяется необходимым расположением функциональных узлов.

В отношении угловых размеров также используется понятие допуска, аналогичное допуску на линейный размер.

Допуском угла называется разность между наибольшим и наименьшим предельными допускаемыми углами. Допуск угла обозначается AT.

При нормировании точности угловых размеров не применяется понятие "отклонение". Предусматривается, что допуск может быть расположен по- разному относительно номинального значения угла (рис.7.2). Допуск может быть расположен в плюсовую сторону от номинального угла (+ АТ), или в минусовую (-AT), или же симметрично относительно нулевой линии (±АТ/2). В первом случае нижнее, а во втором случае верхнее отклонения равны нулю, т.е. аналогично случаю отклонений как для основного от­верстия и основного вала при нормировании точности линейных размеров.

Особенность изготовления и измерения угловых размеров заключается в том, что точность угла в значительной мере зависит от длины сторон, образующих этот угол. И в процессе изготовления, и при измерении, чем меньше длина стороны угла, тем труднее сделать точный угол и тем труд­нее его точно измерить. При нормировании требований к точности угла значение допуска задается в зависимости от значения длины меньшей сто­роны, образующей угол, а не от значения номинального угла.

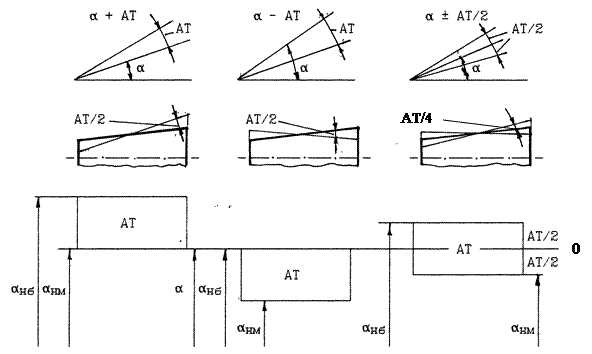
Рис. 7.2. Расположение допуска АТ на угловые размеры относительно

номинального значения угла;α - номинальный угол

2. Способы выражения допуска угла

С учетом того, что значение угла можно выразить несколькими единицами, при нормировании требований к точности значения допуска выражаются разными способами (ГОСТ 2908) и используется разное обозначение (рис.7.3):

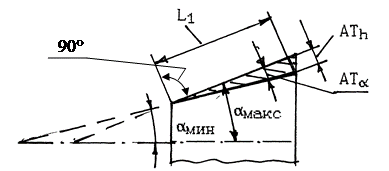
Рис. 7.3. Способы выражения допуска на угловые размеры

AT_α - допуск, выраженный в радиальной мере, и соответствующее ему точное значение в градусной мере;

АТ’_α - допуск, выраженный в градусной мере, но с округленным значением по сравнению с радиальным выражением;

AT_h - допуск, выраженный в линейной мере длиной отрезка на перпендикуляре к концу меньшей стороны угла;

АТ_D - допуск, относящийся только к углу конуса и выраженный в линейной мере, но как разность диаметров на заданном расстоянии в сече­нии конуса плоскостями, перпендикулярными к оси конуса.

В отношении конусов допуск задается чаще всего в зависимости от длины образующей. Когда угол конуса небольшой (конусность не более 1:3), допуск задается в зависимости от длины конуса.

Связь между допусками в угловых и линейных единицах выражается зависимостью

AT_h = AT_α L₁10^-3,

где AT_h - измеряется в микрометрах;

АТ_α - в микрорадианах;

L₁ - длина меньшей стороны угла в миллиметрах.

3. Ряды точности для угловых размеров

В ГОСТ 8908 установлены 17 рядов точности (с 1 по 17, понятие "степень точности" идентично понятиям "квалитет", "класс точности").

Обозначение точности производится указанием условного обозначения допуска на угол и степени точности, например 30° АТ5(^+16" ), на черте­жах предельные отклонения угловых размеров указываются только числовы­ми значениями, например:

60° ± 5’, 30°^{+16 ”}, .

Установлены допуски для углов со стороной до 2500 мм (длина меньшей стороны угла), а первый интервал длин сторон дается для размеров до 10 мм без указания нижнего предела. Интервалы длин сторон для угловых разме­ров не совпадают с интервалами, принятыми для линейных размеров.

4. Нормирование точности конических поверхностей

Размеры конусов могут задаваться различными способами.

Линейные размеры задаются диаметром большого основания D, диаметром малого основания d и длиной конуса L, под которой понимается расс­тояние между основаниями усеченного конуса (рис.7.4).

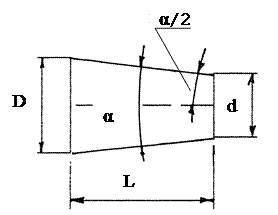
Рис. 7.4. Геометрические параметры конического элемента детали

Угловые размеры конуса могут указываться несколькими вариантами.

Угол конуса α - угол между образующими конуса в сечении конуса плоскостью, проходящей через ось конуса.

Часто вместо угла конуса указывают угол наклона α/2, т.е. угол между образующей и осью конуса. Углы конуса и уклона задаются в гра­дусной мере.

Для стандартизованных конических соединений указанные размеры уг­ла конуса осуществляются чаще всего через понятие "конусность".

Конусность С - отношение разности диаметров большого и малого оснований к длине конуса, т.е.

.

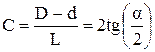Конусность может быть задана и как отношение разности диаметров любых двух поперечных сечений к расстоянию между этими сечениями. Час­то конусность указывают в виде отношения вида1:Х, где Х - расстояние между поперечными сечениями конуса, разность диаметров которых равна 1 мм (например, конусность выраженная как 1:20, т.е. два сечения с раз­ностью диаметров 1 мм отстоят друг от друга на 20 мм).

В машиностроении широко применяются конусы под названием "конус Морзе" с номерами от 0 (ноль) до 6. Наибольшие диаметры у этих конусов находятся приблизительно от 9 мм (Морзе 0) до 60 мм (Морзе 6), а угол конуса, хотя и непостоянен у всех конусов, но близок к углу 3°.

Обозначение конусности на чертеже приведено на рис.7.5.

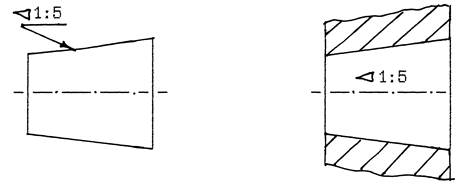
Рис. 7.5. Обозначение конусности на чертеже

Перед размерным числом, характеризующим конусность, наносят знак , острый угол которого должен быть направлен в сторону вершины конуса. Знак конуса и конусность следует наносить в виде соотношения над осевой линией или на полке линии-выноски.

Дата добавления: 2014-01-11