Основы расчета изгибаемых элементов

Классификация нагрузок и их сочетаний

При методике предельных состояний все нагрузки классифицированы в зависимости от вероятности их воздействия на нормативные и расчетные.

По признаку воздействия нагрузки разделяются на постоянные и временные. Последние могут быть длительного и кратковременного воздействия.

Кроме того, есть нагрузки, которые выделяются в разряд особых нагрузок и воздействий.

Постоянные нагрузки – собственный вес несущих и ограждающих конструкций, давление грунта, предварительное напряжение.

Временные длительные нагрузки – вес стационарного технологического оборудования, вес складируемых материалов в хранилищах, давление газов, жидкостей и сыпучих материалов в емкостях и т.д.

Кратковременные нагрузки – нормативные нагрузки от снега, ветра, подвижного подъемно-транспортного оборудования, массы людей, животных и т.п.

Особые нагрузки – сейсмические воздействия, взрывные воздействия. Нагрузки, возникающие в процессе монтажа конструкций. Нагрузки, связанные с поломкой технологического оборудования, воздействия, связанные с деформациями основания в связи с изменениями структуры грунта (просадочные грунты, осадка грунтов в карстовых районах и над подземными выработками).

Существует иногда термин “полезная нагрузка”. Полезной называют нагрузки, восприятие которых составляет цельное назначение сооружений, например, вес людей для пешеходного моста. Они бывают как временными, так и постоянным, например, вес монументального выставочного сооружения является постоянной нагрузкой для постамента. Для фундамента вес всех вышележащих конструкций также представляет полезную нагрузку.

При действии на конструкцию нескольких видов нагрузок усилия в ней определяются как при самых неблагоприятных сочетаниях с использованием коэффициентов сочетаний .

В СНиПе 2.01.07-85 “ Нагрузки и воздействия” различают:

основные сочетания, состоящие из постоянных и временных нагрузок;

особые сочетания, состоящие из постоянных, временных и одной из особых нагрузок.

При основном сочетании, включающем одну временную нагрузку, коэффициент сочетаний 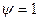. При большем числе временных нагрузок, последние умножаются на коэффициент сочетаний .

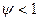В особых сочетаниях временные нагрузки учитываются с коэффициентом сочетаний 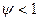, а особая нагрузка - с коэффициентом 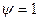. Во всех видах сочетаний постоянная нагрузка имеет коэффициент .

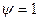2.4. Напряженное и деформированное состояние центрально

нагруженных элементов

Учет сложного напряженного состояния при расчете металлических конструкций производится через расчетное сопротивление 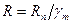, которое устанавливается на основе испытаний металлических образцов при одноосном нагружении. Однако в реальных конструкциях материал, как правило, находится в сложном многокомпонентном напряженном состоянии. В связи с этим необходимо установить правило эквивалентности сложного напряженного состояния одноосному.

В качестве критерия эквивалентности принято использовать потенциальную энергию, накапливаемую в материале при его деформировании внешним воздействиям.

Для удобства анализа энергию деформации можно представить в виде суммы работ по изменению объема А_о и изменения формы тела А_ф. Первая не превышает 13% полной работы при упругом деформировании и зависит от среднего нормального напряжения.

1 - 2υ

A_o = ----------(Ơ_Χ + Ơ_У + Ơ_Ζ)² (2.3.)

6Ε

Вторая работа связана со сдвигами в материале:

1 +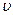

А_ф = -------[(Ơ_Χ²+Ơ_Υ²+ Ơ_z²-(Ơ_xƠ_y+Ơ_yƠ_z+Ơ_zƠ_x) + 3 (τ_xy²+τ_yz²+ τ_zx²)] (2.4.)

3Е

Известно, что разрушение кристаллической структуры строительных сталей и алюминиевых сплавов связано со сдвиговыми явлениями в материале (движение дислокаций и пр.).

Работа формоизменения (2.4.) является инвариантом, поэтому при одноосном напряженном состоянии Ơ = Ơ имеем А₁ =[(1 + 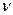) / 3Е ] Ơ²

Приравнивая это значение выражению (2.4) и извлекая квадратный корень, получим:

Ơ_пр=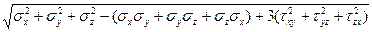=Ơ (2.5)

Это соотношение устанавливает энергетическую эквивалентность сложного напряженного состояния одноосному. Выражение в правой части иногда называют приведенным напряжением Ơ_пр, имея в виду приведение к некоторому состоянию с одноосным напряжением Ơ.

Если предельно допустимое напряжение в металле (расчетное сопротивление) устанавливается по пределу текучести стандартного образца Ơ_T, то выражение (2.5) принимает вид Ơ_пр = Ơ_T и представляет собой условие пластичности при сложном напряженном состоянии, т.е. условие перехода материала из упругого состояния в пластичное.

В стенках двутавровых балок вблизи приложения поперечной нагрузки

Ơ_x 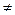0. Ơ_y 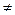0. τ_xy 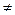0. остальными компонентами напряжений можно пренебречь. Тогда условие пластичности принимает вид

Ơ_пр =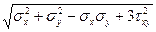= Ơ_T (2.6)

В точках, удаленных от места приложения нагрузки, можно пренебречь также локальным напряжением Ơ _y = 0, тогда условие пластичности еще более упростится: Ơ_пр = 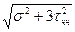= Ơ_T.

При простом сдвиге из всех компонентов напряжений только

τ_xy 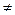0. тогда Ơ_пр = 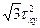= Ơ_T. Отсюда

τ_xy= Ơ_T /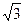= 0,58 Ơ_T (2.7)

В соответствии с этим выражением в СНиПе принято соотношение между расчетными сопротивлениями на сдвиг и растяжение ,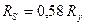

где 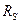- расчетное сопротивление сдвигу; 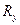- предел текучести.

Поведение под нагрузкой центрально растянутого элемента и центрально сжатого при условии обеспечения его устойчивости полностью соответствует работе материала при простом растяжении-сжатии (рис.1.1, б).

Предполагается, что напряжения в поперечном сечении этих элементов распределяются равномерно. Для обеспечения несущей способности таких элементов необходимо, чтобы напряжения от расчетных нагрузок в сечении с наименьшей площадью не превышали расчетного сопротивления.

Тогда неравенство первого предельного состояния (2.2) будет

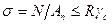, (2.8)

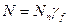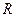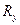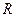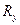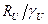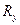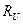где - продольная сила в элементах; - площадь нетто поперечного сечения элемента; - расчетное сопротивление, принимаемое равным , если в элементе не допускается развитие пластических деформаций; если же пластические деформации допустимы, то равняется наибольшему из двух значений и (здесь и - расчетные сопротивления материала по пределу текучести и по временному сопротивлению соответственно); 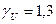- коэффициент надежности по материалу при расчете конструкции по временному сопротивлению; 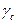- коэффициент условий работы.

Проверка по второму предельному состоянию сводится к ограничению удлинения (укорочения) стержня от нормативных нагрузок

N_n l / (E A) 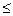∆ (2.9)

где 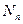- продольная сила в стержне от нормативных нагрузок; 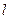- расчетная длина стержня, равная расстоянию меду точками приложения нагрузки к стержню; 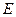- модуль упругости; 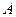- площадь брутто поперечного сечения стержня; 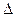- предельная величина удлинения (укорочения).

Для изгибаемых элементов (балок), у которых пролет превышает высоту поперечного сечения (в 5 и более раз) изменение деформаций по высоте

сечения происходит по линейному закону, напряжения распределяются только до предела текучести Ơ_T (рис.2.1).

Напряжения в точках, находящихся на расстоянии “y” от нейтральной оси, определяются по формуле Ơ = М y / I_x, где 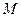- изгибающий момент в рассматриваемом сечении балки; I_x - момент инерции сечения.

Максимальное напряжение возникает когда 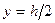: Ơ_max. = М(h/2)/I_x. Отношение момента инерции I_x к расстоянию от нейтральной оси до крайней

Точки сечения 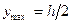называется моментом сопротивления W_x = I_x(2/h), тогда Ơ_max = M/W_x..

Для проверки прочности изгибаемых элементов, работающих в пределах упругих деформаций, необходимо, чтобы максимальные нормальные и касательные напряжения в балке от расчетной нагрузки не превосходили соответствующих расчетных сопротивлений.

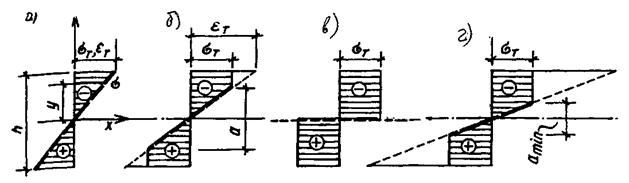Рис.2.1. Изменение эпюры напряжений в изгибаемом элементе при развитии

Дата добавления: 2014-01-13