Некоторые задачи математического программирования

Г. Зойтендейк. Методы возможных направлений. М. – 1963г. 174с.

Основные направления:

1. Прикладные или технологические проблемы: построение математических моделей, сбор данных, интерпретация и анализ результатов

2. Математические проблемы: развитие математических методов для определенных классов задач

3. Вычислительные проблемы: изучение вычислительных схем методов для определенных классов задач, совершенствование соответствующих вычислительных программ

Классы задач:

1. детерминированные непрерывные модели. Совокупность точек, удовлетворяющих ограничениям (допустимая область), связна, оптимизируемая функция непрерывна (Линейное программирование; квадратичное программирование, изучающее задачи минимизации выпуклой квадратичной функции при линейных ограничениях; задачи минимизации выпуклых функций общего вида при линейных ограничениях; выпуклое программирование, которое изучает задачу отыскания минимума выпуклой функции (или максимум вогнутой) на выпуклом множестве)

2. детерминированные разрывные модели. Допустимая область несвязна или (и) оптимизируемая функция разрывная (Целочисленное линейное программирование, решение должно удовлетворять дополнительному условию – состоять из целых чисел; смешанные дискретно-непрерывные задачи – только часть переменных оптимального решения должна удовлетворять условию целочисленности)

3. стохастические модели. Коэффициенты ограничений или (и) оптимизируемой функции - случайные величины (задачи со случайными ограничениями, например, задача линейного программирования со случайным вектором ограничений или случайным целевым вектором)

4. динамические модели. Коэффициенты ограничений или (и) оптимизируемой функции зависят от параметра (например, от времени). Задача должна быть решена для каждого значения параметра.

Задача комбинаторной оптимизации

Комбинаторные постановки задач часто могут быть описаны в виде:

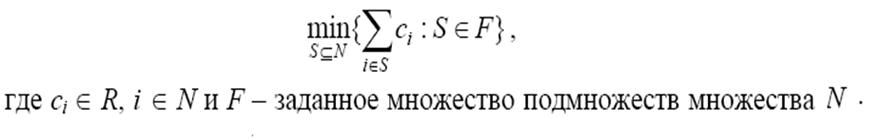
Задача планирования производства

Вид сырья	Нормы расхода сырья (кг) на одно изделие	Общее количество сырья на складе (кг)
А	В
I II III
Прибыль от реализации одного изделия (у.е.)

Для производства 2–х видов изделий предприятие использует 3 вида сырья. Учитывая, что изделия А и В могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий будет максимальной. Предположим, что предприятие изготовит х₁ изделий вида А и х₂ изделий вида В. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьем каждого вида, и количество изготовленных изделий не может быть отрицательным, должны выполняться следующие условия: 1) х_1, х₂ ³ 0 2) 12х₁ + 4 х_{2 £} 300 4 х₁ + 4 х_{2 £} 120 13 х₁ + 12 х_{2 £} 252 Максимальная прибыль от реализации х₁ изделий вида А и х₂ изделий вида В составит m(х) = max (30 х₁ + 40 х₂ ) x

Задача об оптимальной смеси

Цель – подобрать оптимальный состав коктейля из трех компонентов: коньяка, шампанского и сока. Стоимости ингредиентов смеси соответственно: с1=50, с2=100, с3=20; Содержание в них алкоголя: а1=0,4; а2=0,5; а3=0,0; Вкусовые качества в баллах: в1=4, в2=8, в3=10.

Пусть хi(i = 1,2,3) – доля каждого компонента в коктейле (все расчеты ведем на единицу объема). Стоимость коктейля определится функцией: f1(x1, x2, x3)= с1 x1+ с2 x2+ с3 x3 Крепость коктейля определится функцией: f2(x1, x2, x3)= a1 x1+ a2 x2+ a3 x3 Вкус коктейля определится функцией: f3(x1, x2, x3)= в1 x1+ в2 x2+ в3 x3 Естественное желание – получить коктейль минимальной стоимости, максимальной крепости и максимального вкуса (противоречивые критерии!)

Задача об оптимальной смеси (продолжение)

Выберем критерий – оптимизация стоимости, а остальные критерии ограничим на требуемом уровне:

Крепость ограничим долей алкоголя в 0,2, а вкус – 8 баллами.

При этом должны выполняться следующие условия:

1) х_i ≥ 0 (i = 1,2,3)

2) 0,4 x₁+ 0,5 x₂+ 0 x₃ ≥ 0,2

4 x₁+ 8 x₂+ 10 x₃ ≥ 8

x₁+ x₂+ x₃ =1

Минимальная стоимость составит

m(х) =min (50 x₁+ 100 x₂+ 20 x₃)

x

Дата добавления: 2014-01-13