Интеллектуальные модели АИМС

Структура активной информационной мониторинговой системы

Особенности построения активных информационных мониторинговых систем

Лекция № 7.

1. При принятии решений в управлении объектами и процессами в различных трудно формализуемых областях деятельности (экономика, образование, медицина, экология, геология и т.д.) возникает проблема продуктивного анализа априорных данных. Отмеченные объекты относятся к классу сложных систем [1], эффективное управление которыми, было и остается актуальной проблемой, требующей своего решения.

Современный алгоритмический и программный инструментарий, позволяет оперативно конструировать нейросетевую среду, реализовать широкий класс архитектур нейросетей различной сложности и правил модификации синаптического пространства [2]. Сегодня создаются модели продуктивных СППР на основе методов, технологий и программного обеспечения построения схем, позволяющих автоматизировать базовые процессы при распознавании состояний, прогнозировании динамики поведения и выборе оптимальных управляющих факторов исследуемых объектов на базе интеллектуальных технологий [3].

Разработкой, теоретическим обоснованием и внедрением информационных технологий на основе искусственного интеллекта для эффективного управления занимались отечественные и зарубежные ученые, в частности: Глушков В.М., Т. Кохонен, С. Хайкин, Р. Хехт-Нильсен и др. [4, 5, 6, 7]. Вопросами нейроуправления и оптимизации алгоритмов модификации синаптического пространства нейросетей при моделировании различных объектов и процессов занимались Галушкин А.И., Горбань А.Н., Миркес Е.М., и др. [8, 9, 10]. Их труды позволили сегодня говорить о разработанной технологии построения продуктивного ансамбля нейросетевых моделей нахождения такого набора входных факторов, который оптимально надежно и быстро позволяет привести объект в целевое состояние.

С точки зрения формализации процесса распознавания объекта необходимо построить отображение входного вектора данных на результат экспертизы, аппроксимирующее зависимость “поведение - вывод”. В общем случае признаки поведения и число классов объектов являются векторными величинами:

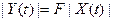, (1)

где 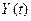– номер класса состояния объекта;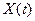– вектор текущих значений входных признаков; 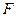– функционал преобразования массива признаков в номер класса.

Задача адаптации входного вектора к требуемому состоянию ССТС состоит в нахождении оптимального набора входного вектора факторов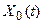, соответствующего вектору целевого состояния 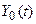объекта исследования.

Этот процесс может быть формально представлен последовательностью процедур:

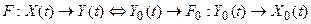, (2)

где 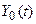– целевой вектор состояния объекта; 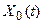– вектор адаптированных значений входных признаков; 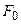– продуктивный функционал модификации массива текущих входных факторов к искомому набору, адекватному целевому состоянию.

Реализация алгоритма (2) позволяет найти оптимальный набор входных факторов как последовательное решение прямой и обратной задачи распознавания состояний ССТС. Решение обратной задачи в нейросетевом формате обеспечивает нахождение таких значений сигналов на входе обученной сети, при которых достигается выходное состояние, соответствующее нужному классу [3].

Решение обратной задачи распознавания состояний исследуемого объекта. Если актуальное состояние объекта не совпадает с требуемым, необходимо найти соответствующий набор входных факторов и привести его в это состояние. Для решения этой задачи следует найти функциональную зависимость состояний от входных факторов.

При этом минимизация целевой функции в постановке задачи выполняется итерационно в процессе обучения сети по алгоритму обратного распространения ошибки (или иным его модификациям) [5] применительно к входным данным исследуемого объекта:

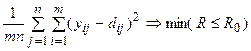, (3)

где y_ij – вектор индикатороввыходныхсостояний; d_ij – результат обучения сети на j- выходе, при i- м примере обучающей выборки; j = 1, n –номер выхода сети; i = 1, m –номер примера; m, n – размерность массива примеров и числа выходных элементов сети;

R₀ – допустимые ограничения по условию задачи.

В нейросетевом формате обучение заканчивается формированием ансамбля нейросетевых моделей. Анализ профилей результатов моделирования позволил выделить сети с приемлемыми для практики производительностью и ошибками на обучающих, контрольных и тестовых множествах. Установленная регрессионная зависимость определяет связь входных факторов и выходных индикаторов системы, через массивы синаптических коэффициентов обученных нейросетевых моделей. Вариации входными факторами позволяют получать различные значения функции, что обеспечивает системного менеджера данными для принятия решений. Однако, актуальное состояние объекта обычно не совпадает с требуемым. Тогда на основании гипотезы компактности не совпадают и признаковые пространства, соответствующие этим состояниям. Поэтому требуется такой набор признаков, который максимально сближал бы классы текущего и требуемого состояний ССТС. Это задача обратная распознаванию образов [3]. После формализации процедур оценки текущего состояния и функциональной зависимости “вход-выход”, решалась задача формализации выбора оптимального признакового пространства в границах установленных дисциплинирующих условий. При небольшом числе изменяемых факторов (3-4) эта задача решалась простым перебором. В случае большого числа факторов (десятки – сотни) целесообразно воспользоваться одним из существующих градиентных методов адаптации входного вектора к заданной функции на выходе [5].

Имея заданный ответ и ответ выданный сетью, вычисляется градиент функции ошибки по входным сигналам сети по известной технологии метода нагруженных двойственных сетей [9]. В соответствии со значениями элементов градиента должны изменяться значения входных сигналов сети в направлении снижения ошибки, что позволяет итерационно получить вектор входных сигналов, порождающих требуемый ответ. При этом синаптическая карта сети (на время адаптации) остается неизменной.

В первой фазе нейроэмулятор должен приобрести свойства инверсной динамики объекта, чтобы в первом приближении отображать динамику поведения объекта. Для этого вначале проводят обучение нейронной сети (нейроэмулятора) в автономном режиме при многоразовой коррекции синаптического пространства. В процессе обучения при необходимости применяется обогащение выборки, выбор наиболее информативных признаков (редукция), выбор оптимальной архитектуры и метода обучения. Как результат сеть выдает отклик требуемой точности или подлежит модификации (увеличивается число задержанных сигналов добавлением соответствующего числа входов сети). Окончанием процесса является достижение адекватности модели в заданных границах установленных показателей.

Для уменьшения риска переобучения нейроэмулятора коэффициенты скорости НЭ уменьшают несколько раз в сравнении с соответствующими коэффициентами для нейроконтроллера.

После достижения необходимой точности автономной реакции НК проводится дополнительное обучение обоих нейросетей на примерах управления ССТС при различных значениях уставки.

Вторая фаза обучения нейросетей системы нейроуправления проходит в рабочем режиме управляемого объекта. Главным является темп операций управления объектом, что обусловливает поступление реализаций Y(t), U(t) Z(t). Каждая новая реализация пополняет обучающую выборку для оперативного обучения.

Состояние объекта отслеживается контроллером, определяющим правильность его реакции на управляющие факторы, задавая управление Z.

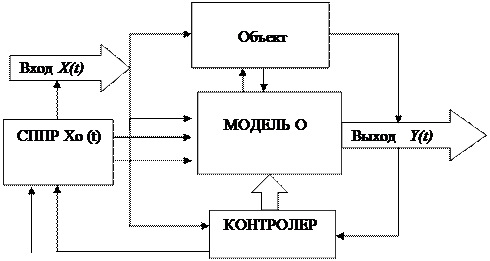
Уставка

Рис.1. Структура процесса адаптации входного вектора

В основе решения задачи лежит приведение ошибки обучения нейронной сети к входному слою нейронов и расчету частных производных градиента функции ошибки по параметрам нейросети и входным факторам. Градиентный спуск приводит к одному из возможных решений обратной задачи. Реализация осуществляется с применением построения нейросетевой модели и её обучение по методу нагруженной сети [9]. Метод позволяет вычислить производных выходной функции невязки текущего и требуемого состояний О по каждому элементу вектора входных факторов и запомнить их. При обратном функционировании эти ранее вычисленные производные, участвуют для вычисления градиентов по входным сигналам сети [5].

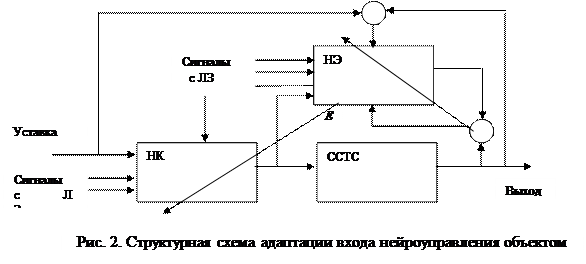
2. Адаптивная система контроллера решает задачу сближения текущего значения выхода с требуемым, заданным вектором уставки. На рис.2 представлена одна из схем нейроуправления объектом. Нейроэмулятор выполняет функции адаптивной модели управляемого объекта. На его входы поступают текущие и задержанные во времени значения векторов управления 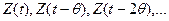и значения разности между векторами входа и уставки 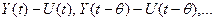. Здесь q - величина шага задержки. Выходом нейроэмулятора является ожидаемое значение выхода управляемого объекта Y*, а также значение вектора ошибки Е для обучения нейроконтроллера.

Z

Y*

Y

Величина 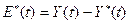представляет вектор ошибки, который используется в алгоритме обучения нейроэмулятора. Ошибка, поступающая в схему контроллера, представляется как ошибка на выходе сети приведенная к первому слою в схеме нейроэмулятора[5, 10]. На вход НЭ поступают:

· Y(t) – текущие значения процесса на выходе;

· Y(t-q) – текущие значения процесса задержанные на один такт q;

· U(t) - Y(t) – текущее значение невязки на выходе системы;

· Z(t) – текущее управляющее воздействие.

Выходом нейроэмулятора являются значения выхода модели ССТС Y*(t).

При обучении НЭ осуществляется модификация синаптического пространства путем подстройки весовых коэффициентов в направлении антиградиента невязки.

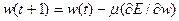, (4)

где 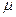- коэффициент обучения; 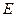– функция невязки (ошибка).

Обозначим ошибку НЭ как: 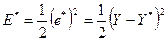, где 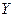- выход ССТС, (5)

а 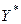– реакцию НЭ: 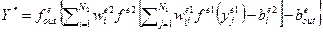, (6)

где 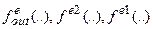– сигнальные (активационные) функции нейронов 2-го та 1-го слоев; 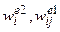– весовые коэффициенты нейронов на участках между нейронами 2-3-го и 1-2-го слоев; 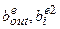– величины порогов нейронов выхода и скрытого слоя.

Для нейронов на входе используется линейная сигнальная функция, а для скрытого слоя – сигмоидная. Порог на выходе обычно равен нулю. Для оценки производной функции невязки выполись действия по известной методике [5, 9]:

На выходе НЭ нейроемулятора процесс формализуется выражением:

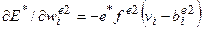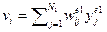, где . (7)

Для связей между входами и скрытым слоем производная ошибки по весам имеет вид:

, (8)

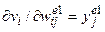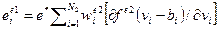где ; . (9)

Величина 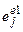представляется ошибкой, приведенной к j -му входу нейроэмулятора. Для входа, на который поступает вектор управления Z, эта величина представляет ошибку реакции НК e^c, которая используется для коррекции синапсов НК. Подставляя полученные значения градиентов невязки в исходное выражение (3), получаем алгоритм модификации весовых коэффициентов НЭ:

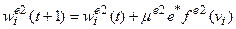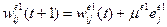; , (10)

где величина 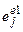рассчитывается по формуле (9). По такому же алгоритму осуществляется и подстройка весовых коэффициентов НК с учетом принятых обозначений входов и выходов.

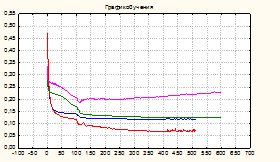
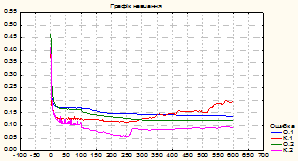
Рис. 3. Обучение моделей ВНС и РБФ

Моделирование градиентного спуска с оценкой частных производных, как по параметрам сети, так и по входным сигналам, представляющим пространство признаков текущего состояния объекта, показало устойчивую сходимость итерационного процесса обучения сети с приемлемыми показателями качества.

Таким образом, при активном мониторинге сложного объекта для расчета входных факторов, приводящих текущее состояние объекта целевому, необходимо найти функциональную зависимость её состояний от значений. Эта задача решается применением технологий нейроуправления и реализуется моделями многослойных персептронов как обратная задача распознавания.

Расчет частных производных по входным факторам выходной функции невязки текущего и требуемого состояний объекта выполненяются на основе известных свойств нейросетевых схем. Это позволяет автоматизировать процесс определения элементов вектора градиента при реализации традиционного метода обратного распространении ошибки.

Литература

1. Бусленко Н.П. Моделирование сложных систем. –М.: Наука, 1978. –400 с.

2. Боровиков В.П. STATISTICA NN - Техническое описание. М.: Мир,1999. – 239 с.

3. Морозов А.А. Состояние и перспективы нейросетевого моделирования СППР в сложных социотехнических системах / А.А. Морозов, В.П. Клименко, А.Л. Ляхов, С.П. Алёшин // Математичні машини і системи. – 2010. - № 1.- С. 127 – 149.

4. Кохонен Т. Ассоциативная память. - М.: Мир, 1980.- 384 с.

5. Хайкин С. Нейронные сети: полный курс – [2-е изд.]; пер. с англ. – М.: Издательский дом «Вильямс», 2006. – 1104 с.

6. Хехт-Нильсен Р. Нейрокомпьютинг: история, состояние, перспективы / Р. Хехт-Нильсен // Открытые системы. – 1998. – № 4. – С. 10 – 14.

7. Глушков В.М. Кибернетика, вычислительная техника, информатика: в 3 т. – Т. 2: ЭВМ – техническая база кибернетики. – Киев: Наукова думка, 1990. – С. 140 – 177.

8. Галушкин А.И. Нейрокомпьютеры и их применение на рубеже тысячелетий в Китае. – М., 2004. – Т. 1. – 367 с.; Т. 2. – 464 с.

9. Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере // Новосибирск: Наука, 1996.- 276 с.

10. Миркес Е.М. Нейрокомпьютер. Проект стандарта.- Новосибирск: Наука, Сибирская издательская фирма РАН, 1998.- 337 с.

Дата добавления: 2014-01-13