Энтропия источника с попарной зависимостью сообщений

Учебные вопросы занятия

Лекция № 4. Информационные характеристики источников сообщений.

ЛЕКЦИЯ

Защиты информации

по учебной дисциплине "Теория информации "

для студентов специальности 075500 (090105) – Комплексное обеспечение информационной безопасности автоматизированных систем

.

Ставрополь 2009 г.

Цель занятия: Изучить информационные характеристики дискретных источников сообщений. Ознакомиться с энтропией зависимых и непрерывных событий. Изучить информационные пределы избыточности.

1.Энтропия источника с попарной зависимостью сообщений.

2. Информационные пределы избыточности

.

Количество информации, содержащейся в одном элементе А_i выбираемого из алфавита {A_i}где i = 1..n, где n объем алфавита, определяется следующим выражением

J(А_i) =-log₂P(А_i) = H(А_i), (1).

где Р(А_i) – вероятность появления i-го элемента алфавита, H(А_i) - частная энтропия.

Частная энтропия определяет информативность элемента алфавита для «неподготовленного» получателя, и совершенно не учитывает как смыслового содержания, так и субъективную ценность передаваемого сообщения. Таким образом, в основе информационной характеристики дискретного источника лежит только вероятностный характер источника сообщений.

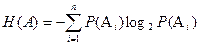Тогда средняя частная энтропия источника сообщения, приходящая на один элемент, выдаваемый дискретным источником независимых элементов с объемом алфавита М, можно найти как математическое ожидание дискретной случайной величины H(А_i), т.е.будет определяться следующим равенством

Данное выражение справедливо при условии, что все элементы алфавита независимы. На самом деле элементы алфавита генерируются взаимозависимыми, ограничимся рассмотрением парной зависимости.

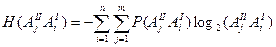Пусть заданы вероятности появления элементов А_i^I и A_j^II т.е. Р(А_i^I) Р(A_j^II) причем эти вероятности равны если i = j. Также дана условная вероятность появления элемента A_j^II при условии, что ранее был передан элемент А_i^I, т.е. Р(A_j^II/A_i^I) тогда условная энтропия приходящаяся на пару символов алфавита определяется следующим образом

где Р(A_j^IIA_i^I) вероятность парного появления (A_j^IIA_i^I).

Известно что Р(A_j^IIA_i^I) = P(A_i^I) Р(A_j^II/A_i^I) подставляя данное выражение в предыдущее, получаем

Полученное выражение соответствует энтропии на сочетание элементов во взаимозависимых источниках. Для вычисления энтропии источника с взаимозависимыми элементами необходимо разделить полученный результат на два.

Дата добавления: 2014-01-13