Энергия электромагнитного поля

1.9.1. Основные гипотезы. Энергия представляет собой количественную меру движения материи. Закон сохранения энергии – один из фундаментальных законов природы. Явления электромагнетизма также подчиняются этому закону. В равной степени электромагнитное поле подчиняется закону сохранения массы, связанной с энергией универсальным соотношением W = mc ², и закону сохранения импульса. Поэтому, рассматривая в дальнейшем энергетические характеристики движущегося электромагнитного поля, будем иметь в виду, что аналогичные соотношения справедливы для массы поля, являющейся важнейшим свойством материи, и импульса поля.

Известно, что закон сохранения энергии в механике используется для решения многих задач о движении и состоянии тел. Формулы для кинетической и потенциальной энергии дают возможность описать характерные особенности перехода механической системы из одного состояния в другое, не вникая в де­тальное описание этого процесса. Можно утверждать, что соотношения, определяющие сохранение энергии электромагнитного поля, столь же полезны для анализа электромагнитных процессов, как и соответствующие формулы в механике.

Говоря о реальности электромагнитного поля, подразумевают, что с полем связана энергия. Изменяясь, поле может отдавать энергию какому-либо неэлектромагнитному процессу, а также отбирать энергию. Величину энергии электромагнитного поля, запасённой в некотором объёме V, принято обозначать буквой W. Объемная плотность энергии электромагнитного поля обозначают через w.

Макроскопическая теория поля основана (кроме уравнений Максвелла) на следующих понятиях, устанавливающих связь между векторами поля и его энергетическими характеристиками:

1. Электромагнитная энергия распределена в пространстве с объемной плотностью:

w = w _э + w _м, (1.39)

где w _э – объемная плотность энергии электрического поля, а w _м – объемная плотность энергии магнитного поля, которые определяются по следующим формулам:

. (1.40)

Величина w имеет размерность Дж/м³ или Вт×с/м³.

Энергия электромагнитного поля, запасённая в объёме V, вычисляется по следующей формуле:

, [Дж].

2. Плотность потока электромагнитной энергии равна векторному произведению напряженностей электрического и магнитного полей:

, (1.41)

где – вектор Пойнтинга, указывающий направление движения энергии и равный по величине плотности ее потока.

Плотность потока энергии равнозначна плотности мощности, т.е. мощности электромагнитной волны, проходящей через единичную площадку, перпендикулярную направлению ее распространения. Размерность вектора Пойнтинга Вт/м².

Объемная плотность энергии w характеризует состояние электро­магнитного поля в данной точке пространства, а вектор Пойнтинга – волновое движение поля через эту точку. При этом скорость переноса энергии электромагнитной волной 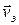определяется по следующей формуле:

. (1.42)

1.9.2. Баланс энергии электромагнитного поля. Пусть сторонние источники , возбуждающие электромагнитное поле во всём пространстве, находятся в конечном объёме V, ограниченном поверхностью S. Тогда для этого объёма имеет место соотношение, называемое теоремой Умова-Пойнтинга в интегральной форме

, (1.43)

где Р _ст– мощность сторонних источников в объёме V; Р _п – мощность тепловых потерь в объёме V; Р_å – мощность излучения из V, она характеризует обмен энергией между объёмом V и окружающей средой; W – величина энергии, запасенной в V.

Величины, входящие в формулу (1.43), связаны с векторами электромагнитного поля следующими соотношениями:

, , , (1.44)

де Р _ст, Р _п, Р _S измеряются в Вт.

Формула (1.43) выражает баланс мощности (энергии) в ограниченном объёме V. Из этого соотношения следует, что мощность сторонних источников расходуется на мощность потерь, мощность излучения из объема V и мощность, расходуемую на изменением энергии, запасённой в объеме V.

1.9.3. Баланс энергии монохроматического поля. В случае монохроматических полей мгновенные значения плотности энергии и мощности меняются периодически в каждой точке пространства. Физическую сущность процесса позволяют установить средние за период значения энергетических характеристик электромагнитного поля, которые будем обозначать с помощью индекса «ср».

Для монохроматических полей имеет место уравнение баланса комплексной мощности

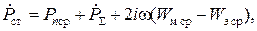(1.45)

где Р_{n ср} – средняя за период мощность джоулевых потерь; – комплексная мощность излучения через замкнутую поверхность S, ограничивающую объём V; – комплексная мощность сторонних источников, расположенных в объёме V; W _{э ср}, W _{м ср} – средние за период значения электрической и магнитной энергии, запасённой в объёме V.

Величины, входящие в (1.45), связаны с комплексными амплитудами векторов электромагнитного поля следующими соотношениями:

, , ,

,.

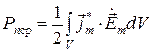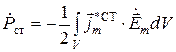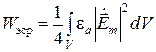В последних соотношениях знак (*) означает комплексно-сопряжённую величину.

Комплексный вектор Пойнтинга 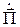определяется формулой

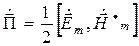. (1.46)

Вещественная часть комплексного вектора Пойнтинга равна среднему за период значению вектора Пойнтинга , которое можно рассматривать как среднюю за период плотность потока энергии (мощности).

Отделяя в соотношении (1.45) действительную часть и мнимую часть, получаем следующие соотношения:

Р _{ст ср}= Р_{n ср}+ Р _åср, (1.47)

. (1.48)

Соотношение (1.47) является уравнением баланса для средней за период (активной) мощности, а соотношение (1.48) – уравнением баланса реактивной мощности. При этом

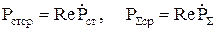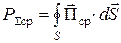, . (1.49)

Из формулы (1.47) следует, что средняя за период мощность сторонних источников расходуется на среднюю мощность потерь и среднюю мощность излучения. Сравнив уравнения (1.43) и (1.47), обнаружим отсутствие в (1.47) слагаемого, соответствующего изменению запаса энергии в рассматриваемом объеме. Это объясняется тем, что в гармонически изменяющемся поле средняя плотность энергии в каждой точке неизменна, так как в каждой точке напряженности поля периодически принимают одни и те же значения.

Из формулы (1.48) следует, что реактивная мощность сторонних источников «складывается» из реактивной мощности излучения (реактивный поток энергии через границу S) и величины, пропорциональной разности средних за период энергий магнитного и электрического полей, запасенных в рассматриваемом объеме.

Скорость волны в линейной среде, как и скорость света, не зависит от интенсивности полей; следовательно, она одинакова во всех точках и неизмен­на в течение периода колебания. Поэтому из формулы (1.42) следует, что

, (1.50)

где w _ср – средняя объемная плотность энергии волны, которая складывается из средней объемной плотности электрической w _эср и магнитной w _мср энергии. При этом

.

Из формулы (1.50) следует, что энергетическая скорость гармонической волны равна отношению среднего вектора Пойнтинга к средней объемной плотности энергии волны.

Раздел 2

Дата добавления: 2014-01-13