Плоские электромагнитные волны в среде без потерь

Рассмотрим вначале случай, когда потери в среде отсутствуют, т.е. когда s = 0, . В этом случае комплексные волновое число и волновое сопротивление среды являются вещественными величинами и соответственно равны

. (2.4)

Отметим, что в случае вакуума Z_c = 120p» 377 Ом.

В этом случае уравнения (2.1) и (2.2) имеют вид:

, (2.5)

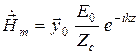. (2.6)

Перейдем во временную область, т.е. найдем действительные векторы монохроматического поля, соответствующие комплексным амплитудам (2.5) и (2.6). Используя формулу (1.28), получаем следующие выражения:

, (2.7)

(2.8)

Выражения (2.7) и (2.8) и определяют (описывают), как будет видно из их анализа, так называемую плоскую электромагнитную волну в свободном пространстве без потерь. Проанализируем формулы (2.7) и (2.8).

1. Векторы 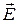и 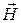перпендикулярны друг другу.

2. Рассмотрим 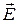и для фиксированного момента времени. Пусть t = 0, тогда векторыи зависят только от пространственной координаты z
(см. рис. 2.1).

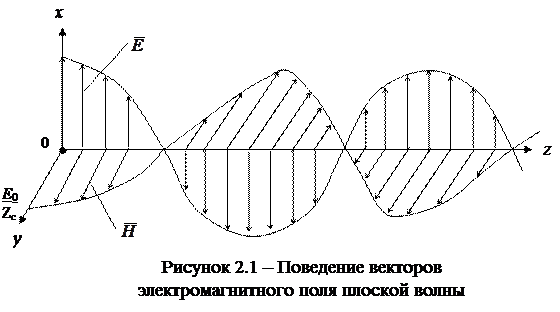Для другого момента времени t ₀ > 0 «картина», представленная на рис. 2.1, переместится вдоль оси z на некоторое расстояние. Таким образом, с течением времени рассматриваемая «картина» распространяется вдоль оси z, т.е. форму­лы (2.7) и (2.8) описывают волновой процесс (волну) в безграничной среде.

3. Фронтом волны называется поверхность равных фаз. Найдем ее. Так как фаза волны равна w t – kz, то ее фронт будет определяться уравнением
w t – kz = const. Отсюда следует, что фронтом волны является любая плоскость
z = const.

Электромагнитные волны (как и волны иной природы) принято клас­сифицировать по структуре ее фронта. Если фронт волны является плоскостью, то волну называют плоской волной, если сферой, то сферической и т.д. Таким образом, выражения (2.7) и (2.8) описывают плоскую электромагнитную волну. Фронт волны перпендикулярен оси z. Отметим, что амплитуды векторов 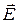и 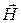не зависят от координат.

Волны, амплитуды которых не меняются по фронту, принято называть однородными плоскими волнами.

4. Фронт волны распространяется вдоль оси z с конечной скоростью. Эту скорость называют фазовой скоростью волны и обозначают через v _ф. Найдем фазовую скорость.

При t = t ₀ фронт волны описывается уравнением вида:

w t ₀ – kz ₀ = const.

При t = t ₀ + D t тот же фронт волны описывается уравнением:

w(t ₀ + D t) – k (z ₀ + D z) = const.

Вычитая из одного равенства другое получаем, что

wD t = k D z. (2.9)

Из последнего соотношения получаем формулу для фазовой скорости волны:

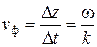. (2.10)

Учитывая выражение (2.4) для волнового числа, получаем, что в среде без потерь фазовая скорость волны равна

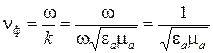. (2.11)

Из последнего выражения следует, что в среде без потерь плоская электромагнитная волна распространяется со скоростью света v ₀. Для вакуума
e _а = e₀, m _а = m₀, а v _ф = c = 3 × 10⁸ м/с.

5. Векторы 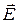и 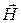перпендикулярны направлению распространения волны. Такая волна называется поперечной волной, или волной типа Т (ТЕМ).

6. Рассмотрим понятие длины волны. Понятие длины волны можно ввести по аналогии с периодом Т = 2p/w, как пространственный период волны с помощью следующей формулы:

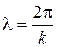. (2.12)

Используя выражение для волнового числа, можно получить формулу, которая связывает длину волны с ее фазовой скоростью

.

7. Из формул (2.7) и (2.8) следует, что амплитуда вектора 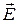в 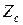раз больше амплитуды вектора 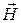. Для вакуума ОM.

8. Вычислим комплексный вектор Пойнтинга:

,

. (2.13)

Из полученной формулы следует, что у плоской волны нет реактивной мощности.

В среднем за период плотность потока мощности плоской волны зависит от амплитуды вектора 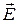и от волнового сопротивления среды.

9. Подставим соотношения (2.5) и (2,6) в формулы (1.40) и учтем формулу (1.39). При этом получим, что среднее значение объемной плотности энергии волны описывается следующим выражением:

.

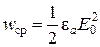10. Найдем скорость движение энергии плоской волны. Разделив соотношение (2.13) на последнее соотношение, получаем:

.

Из последнего выражения следует, что в среде без потерь плоская электромагнитная волна переносит энергию вдоль оси z (перпендикулярно фронту волны) со скоростью света v ₀.

Дата добавления: 2014-01-13