
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Волны в прямоугольном волноводе
|
|
|
|
1. В прямоугольном волноводе (см. рис. 3.7) могут распространяться волны электрического (Е) и магнитного (H) типов. Эти волны принято обозначать как волны Еmn и Hmn. При этом величины m и n могут принимать любые положительные значения.
Отметим, что для волн класса Hmn индекс m либо n может принимать значение нуль.
 |
Отметим также, что индексам m и n, которые определяют тип волны, можно придать четкий физический смысл. Именно, индекс m (n) определяет число стоячих полуволн, укладывающихся вдоль широкой (узкой) стенки волновода.
2. Критическая длина волны как для волн Еmn, так и для волн Hmn, зависит от размеров поперечного сечения волновода, типа волны и может быть определена по формуле
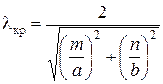 , (3.8)
, (3.8)
где a и b – размеры широкой и узкой стенок волновода.
3. Из формулы (3.8) следует, что в случае a > b величина lкр принимает наибольшее значение при m = 1, n = 0. Отсюда следует, что основным типом волны в прямоугольном волноводе является волна H 10. При этом критическая длина волны H10 равна удвоенному размеру широкой стенки волновода, т.е.
lкр = 2 а. (3.9)
4. Векторы 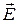 и
и 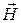 волны H10 в волноводе без потерь определяются следующими формулами:
волны H10 в волноводе без потерь определяются следующими формулами:
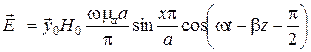 , (3.10)
, (3.10)
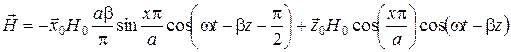 , (3.11)
, (3.11)
где Н 0 – любая постоянная, которая определяется мощностью источников, возбудивших волну,
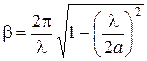 . (3.12)
. (3.12)
5. Из формул (3.10) и (3.11) видно, что в поперечном сечении волновода вектор 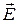 направлен перпендикулярно широкой стенке волновода, вектор
направлен перпендикулярно широкой стенке волновода, вектор 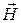 – параллельно. При этом амплитуда вектора
– параллельно. При этом амплитуда вектора 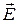 меняется по закону
меняется по закону 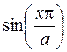 . Она максимальна в точках посреди широкой стенки, и убывает до нуля при приближении к узким стенкам.
. Она максимальна в точках посреди широкой стенки, и убывает до нуля при приближении к узким стенкам.
Поперечные составляющие векторов 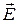 и
и 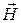 имеют одинаковые фазы, а продольная составляющая вектора
имеют одинаковые фазы, а продольная составляющая вектора 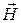 опережает их на 900.
опережает их на 900.
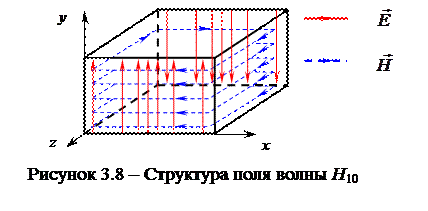 |
На рис. 3.8 показана структура поля волны H 10 (поведение силовых линий векторов
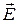 и
и 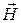 в фиксированный момент времени). При этом пунктирными линиями обозначены силовые линии вектора напряженности магнитного поля, а сплошными – вектора напряженности электрического поля.
в фиксированный момент времени). При этом пунктирными линиями обозначены силовые линии вектора напряженности магнитного поля, а сплошными – вектора напряженности электрического поля.
6. Подставим формулу (3.9) в соотношения (3.5), (3.6) и (3.7), тогда получим, что для основного типа волны прямоугольного волновода:
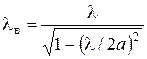 ,
, 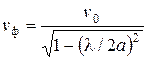 ,
, 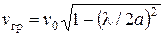 .
.
7. Коэффициент затухания волны Н10 в стенках волновода можно рассчитать по формуле:
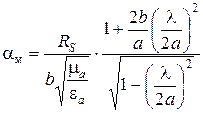 ,
,
где RS – поверхностное сопротивление материала, из которого выполнен волновод, может быть определено по формуле:
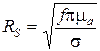 .
.
8. Условие одноволнового режима в прямоугольном волноводе при а ³ 2 b имеет вид
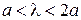 .
.
9. На поверхности стенок волновода протекают поверхностные токи, которые связаны с вектором магнитного поля следующей формулой:
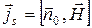 ,
,
где 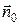 – орт внутренней нормали к стенкам волновода;
– орт внутренней нормали к стенкам волновода; 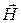 – значение магнитного поля волны на поверхности стенок волновода.
– значение магнитного поля волны на поверхности стенок волновода.
На рис. 3.9. в качестве примера представлена структура токов (силовые линии вектора 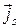 ) для волны Н 10.
) для волны Н 10.
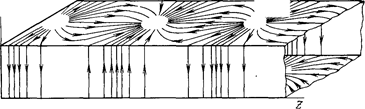
Рисунок 3.9 – Структура токов на стенках волновода для волны Н 10
Распределение тока по стенкам волновода важно знать как при конструировании самого волновода, так и при конструировании волноводных устройств. Большая плотность токов через ребро прямоугольного волновода требует хорошей проводимости этих участков. При создании на базе волноводов устройств различного назначения приходится прорезать в нем узкие щели. Щели не вызывают заметных потерь на излучение и не искажают структуру поля волны, если они расположены вдоль линий тока. Для волны Н10 такими щелями являются поперечные щели на узких стенках и продольная щель, расположенная посредине широкой стенки волновода. На практике часто возникает задача создания излучающей щели, которая является элементом щелевой антенны или используется для ввода энергии в волновод. Излучающая щель хотя бы часть периода пересекается линиями тока.
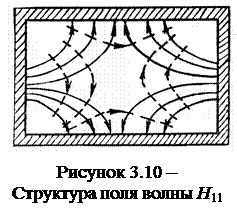
10. Как отмечалось, в прямоугольном волноводе могут распространяться также высшие типы волн, которые могут быть использованы в тех или других волноводных устройствах. Структура поля высших типов волн имеет более сложный характер. В качестве примера на рис. 3.10 и рис. 3.11 представлены в поперечном сечении волновода структуры поля волн Н 11 и Е 11.
 |
 |
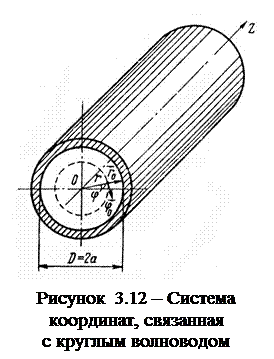 3.5. Волны в круглом волноводе
3.5. Волны в круглом волноводе
Распространение волн в круглом волноводе удобно изучать в цилиндрической системе координат. В этой системе положение вектора в пространстве определяется координатами  и соответствующими ортами
и соответствующими ортами 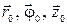 . На рис. 3.12 представлено сечение круглого волновода радиуса
. На рис. 3.12 представлено сечение круглого волновода радиуса 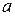 .
.
Рассмотрим особенности распространения волн в круглом волноводе.
1. В круглом волноводе, как и в прямоугольном, могут распространяться волны электрического (Еmn) и магнитного (Нmn) типов. Для круглого волновода критические длины волн зависят от радиуса поперечного сечения волновода, типа волны и могут быть определены по следующим формулам:
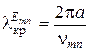 ,
, 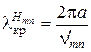 , (3.13)
, (3.13)
где vmn – значение n -го корня функции Бесселя m -го порядка; 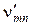 – значение n -гокорня производной функции Бесселя m -гo порядка,
– значение n -гокорня производной функции Бесселя m -гo порядка, 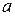 – радиус волновода.
– радиус волновода.
Отметим также, что для круглого волновода индексам m и n, которые определяют тип волны, также можно придать четкий физический смысл. Именно, индекс n определяет число полуволн, укладывающихся от оси волновода до его стенки, а индекс m определяет периодичность поля по полярному углу j.
В табл. 3.1 приведены корни функций Бесселя и ее производной, а также критические частоты волн в круглом волноводе с воздушным заполнением.
Таблица 3.1 – Корни функций Бесселя и ее производной
| Н -волны | Е -волны | ||||
| m – n | n ¢ | 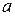 f кр, ГГц см f кр, ГГц см
| m – n | n | 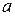 f кр, ГГц см f кр, ГГц см
|
| 1–1 | 1,8412 | 8,7849 | 0–1 | 2,4048 | 11,4743 |
| 2–1 | 3,0542 | 14,5728 | |||
| 0–1 | 3,8317 | 18,2824 | 1–1 | 3,8317 | 18,2824 |
| 3–1 | 4,2012 | 20,045 | |||
| 4–1 | 5,3176 | 25,372 | 2–1 | 5,1356 | 24,504 |
| 1–2 | 5,3314 | 25,438 | 0–2 | 5,5201 | 26,338 |
| 5–1 | 6,4156 | 30,611 | 3–1 | 6,3802 | 30,442 |
| 2–2 | 6,7061 | 31,997 | |||
| 0–2 | 7,0156 | 33,474 | 1–2 | 7,0156 | 33,474 |
2. Из табл. 3.1 и формул (3.13) видно, что критическая частота принимает наименьшее значение (lкр – наибольшее) при m = 1, n = 1. Отсюда следует, что основным типом волны в круглом волноводе является волна H 11. При этом критическая длина волны H 11 определяется по формуле
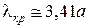 . (3.14)
. (3.14)
3. Проекции векторов 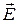 и
и 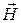 волны Н 11 на орты
волны Н 11 на орты 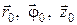 цилиндрической системы координат для случая волновода без потерь имеют вид
цилиндрической системы координат для случая волновода без потерь имеют вид
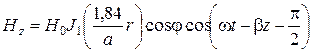 ,
,
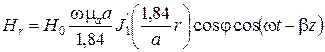 ,
,
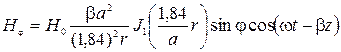 ,
,
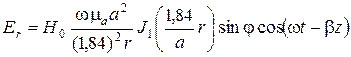 ,
,
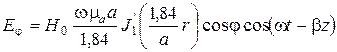 ,
,
где 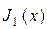 ,
, 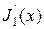 – функция Бесселя первого порядка и ее производная; Н 0 – любая постоянная, которая определяется мощностью источников, возбудивших волну:
– функция Бесселя первого порядка и ее производная; Н 0 – любая постоянная, которая определяется мощностью источников, возбудивших волну:
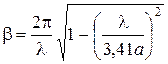 . (3.15)
. (3.15)
4. На рис. 3.13,а показана структура поля волны H 11 в поперечном сечении круглого волновода.
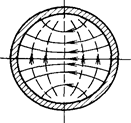 а)
а) 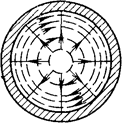 б)
б) 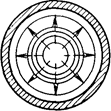 в)
в)
Рисунок 3.13 – а) волна Н11, б) волна Е01, в) волна Н01
5. Отметим, что каждой волне прямоугольного волновода найдется соответствующая волна в круглом волноводе, т.е. такая волна, которая возникает в круглом волноводе при плавной трансформации прямоугольного волновода в круглый. Например, волна Е 01, структура поля которой приведена на
рис. 3.13,б, соответствует волне Е 11 прямоугольного волновода. Обратное не имеет места. В круглом волноводе имеется бесконечное число волн типа Н 0 m ,
m = 1, 2, 3, …., которым нет аналога в прямоугольном волноводе. На рис. 3.13,в приведена структура поля волны Н 01. У стенок волновода этой волны, существует лишь одна составляющая поля Нz, поэтому в стенках существуют лишь кольцевые токи J j. Отсутствие продольных токов делает волны Н  мало чувствительными к поперечным щелям. Возможен, например, небольшой зазор между двумя секциями волновода.
мало чувствительными к поперечным щелям. Возможен, например, небольшой зазор между двумя секциями волновода.
6. Подставим формулу (3.14) в соотношения (3.5), (3.6) и (3.7), тогда получаем, что для основного типа волны круглого волновода
 ,
, 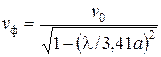 ,
, 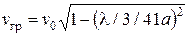 .
.
7. Коэффициент затухания волны H 11 в стенках волновода можно рассчитать по формуле:


8. Условие одноволнового режима в круглом волноводе имеет вид
2,61 а < l < 3,41 a.
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 21216; Нарушение авторских прав?; Мы поможем в написании вашей работы!