Интерполирование сплайнами

Интерполирование многочленом Лагранжа или Ньютона на всем отрезке 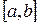с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязано приводить к повышению точности. Для того, чтобы избежать больших погрешностей, весь отрезок 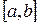разбивают на частичные отрезки и на каждом частичном отрезке приближенно заменяют функцию 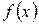многочленом невысокой степени (так называемая, кусочно-полиномиальная интерполяция).

Одним из способов интерполирования на всем отрезке является интерполирование с помощью сплайн-функций. Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную на отрезке 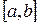и имеющую на этом отрезке некоторое число непрерывных производных.

Преимуществом сплайнов перед обычной интерполяцией является, во-первых их сходимость и, во-вторых, устойчивость процесса вычислений.

Рассмотрим построение кубического сплайна. Пусть на 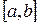задана непрерывная функция 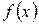. Введем сетку

и обозначим , .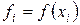

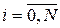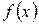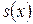Кубическим с плайном, соответствующим данной функции и данным узлам называется функция , удовлетворяющая следующим условиям:

а) на каждом сегменте 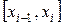, , 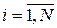функция 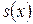является многочленом третьей степени.

б) функция 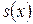, а также ее первая и вторая производные непрерывны на .

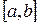в) , .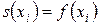

Последнее условие называется условием интерполирования, а сплайн, определяемый условиями а)-в), называется также интерполяционным кубическим сплайном.

Докажем существование и единственность сплайна, определяемого перечисленными выше условиями. Приведенное ниже доказательство содержит также способ построения сплайна.

На каждом из отрезков 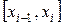, 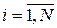будем искать функцию 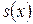=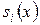в виде многочлена третьей степени

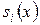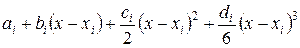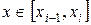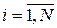=, , , (2.19)

где 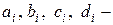коэффициенты, подлежащие определению. Смысл введенных коэффициентов очевиден:

.

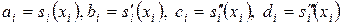Из условий интерполирования 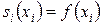, 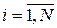. Доопределим, кроме того, .

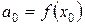Требование непрерывности функции 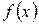приводит к условиям

, ,

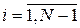отсюда, учитывая выражение для функции 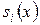, получаем при к уравнения

.

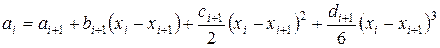Обозначая 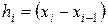, перепишем это уравнение в виде

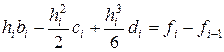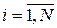, . (2.20)

Условие непрерывности первой производной

,

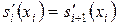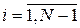
приводят к уравнениям

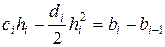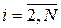, . (2.21)

Из условия непрерывности второй производной, получаем уравнения

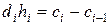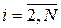, . (2.22)

Объединяя (2.20)-(2.22), получаем систему уравнений относительно 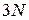неизвестных , .

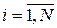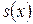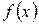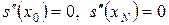Два недостающих уравнения получают, задавая те или иные граничные условия для . Предположим, например, что функция удовлетворяет условию . Тогда естественно требовать, чтобы . Отсюда получаем , т.е. 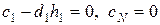. Заметим, что условие 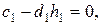совпадает с уравнением (2.22) при 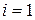, если положить . Таким образом, приходим к замкнутой системе уравнений для определения коэффициентов кубического сплайна:

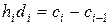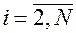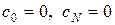, , , (2.23)

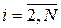, , (2.24)

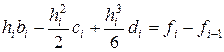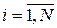, . (2.25)

Методом исключения неизвестных. Получаем

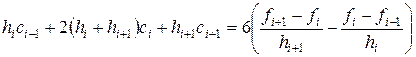, (2.26)

, .

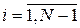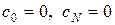Система уравнений (2.26) имеет единственное решение. Матрица полученной системы линейных алгебраических уравнений трехдиагональная. Решение такой системы уравнений можно найти методом прогонки. По найденным коэффициентам 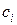коэффициенты 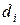определяются с помощью явных формул

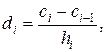
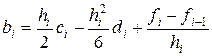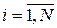, . (2.27)

Итак, существует единственный кубический сплайн, определяемый условиями а)-в) и граничными условиями . Можно рассматривать и другие граничные условия.

Интерполирование кубическими сплайнами является сходящимся процессом. Это означает, что при неограниченном увеличении числа узлов 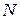соответствующая последовательность сплайн-функций сходится к интерполируемой функции 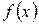. Оценки погрешности интерполяции 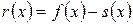зависят от выбора сеток и от гладкости .

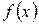Если рассматривать последовательность равномерных сеток

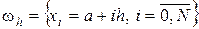
с шагом 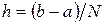. В этом случае система уравнений (2.26)-(2.27) существенно упрощается:

,

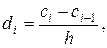
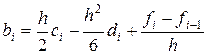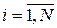, . (2.28)

Можно получить оценку

, (2.29)

где , кубический сплайн, построенный для функции 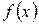на сетке .

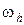Дата добавления: 2014-01-13