Примеры формул численного интегрирования

Численное интегрирование и дифференцирование

В настоящем разделе рассмотрим способы приближенного вычисления определенных интегралов

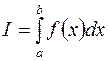, (3.1)

основанные на замене интеграла конечной суммой

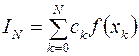, (3.2)

где 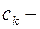числовые коэффициенты и 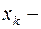точки отрезка 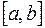, 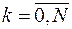. Приближенное равенство

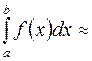
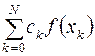
называется квадратурной формулой, а сумма вида (3.2) – квадратурной суммой. Точки 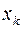называются узлами квадратурной формулы, а числа 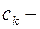коэффициентами квадратурной формулы. Разность

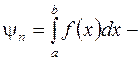
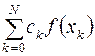
называется погрешностью квадратурной формулы. Погрешность зависит как от выбора узлов, так и от выбора коэффициентов.

Введем на 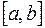равномерную сетку с шагом 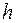, т.е. множество точек

,

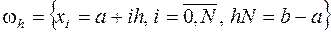и представим интеграл (3.1) в виде суммы интегралов по частичным отрезкам:

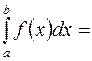
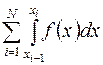. (3.3)

Для построения формулы численного интегрирования на всем отрезке 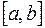достаточно построить квадратурную формулу для интеграла

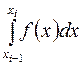(3.4)

на частичном отрезке 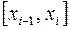и воспользоваться формулой (3.3).

1. Формула прямоугольников. Заменим интеграл (3.4) выражением 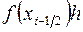, где 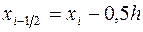. Тогда получим формулу

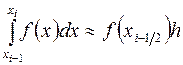, (3.5)

которая называется формулой прямоугольников.

Погрешность метода (3.5) определяется величиной

,

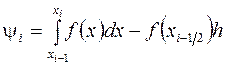которую легко оценить с помощью формулы Тейлора. Действительно, запишем 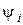в виде

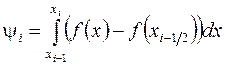(3.6)

и воспользуемся разложением

,

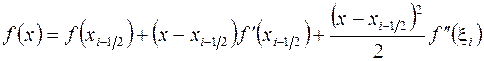где 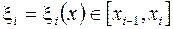. Тогда из (3.6) получим (доказать, дом. зад.№3)

.

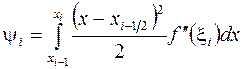Обозначая 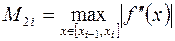, получаем для 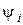следующую оценку (доказать, дом. зад.№3): .

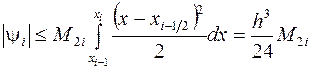Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка

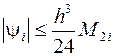, (3.7)

т.е. формула имеет погрешность 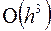при .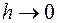

Суммируя равенства (3.5) по 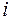от 1 до 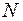, получим составную формулу прямоугольников

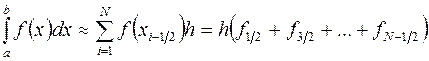. (3.8)

Погрешность этой формулы

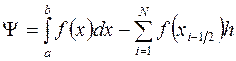
равна сумме погрешностей по всем частичным отрезкам,

.

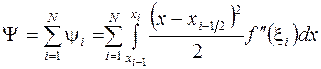Отсюда, обозначая 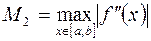, получим

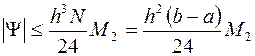, (3.9)

т.е. погрешность формулы прямоугольников на всем отрезке есть величина .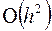

В этом случае говорят, что квадратурная формула имеет второй порядок точности.

2. Формула трапеции. На частичном отрезке эта формула имеет вид

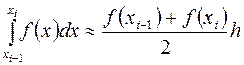(3.10)

и получается путем замены подынтегральной функции 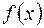интерполяционным многочленом Лагранжа первой степени, построенным по узлам 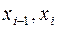, т.е. функцией (доказать, дом. зад.№3,см. формулу 2.4, лекция 1.2)

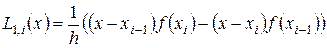
Для оценки погрешности достаточно вспомнить, что (см. формулу 2.5, лекция 1.2)

.

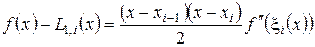Отсюда получим

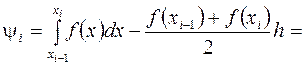
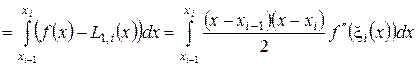
и, следовательно (доказать, дом. зад.№3),

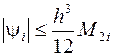. (3.11)

Составная формула трапеции имеет вид

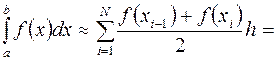
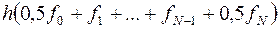, (3.12)

где , , .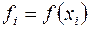

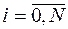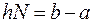Погрешность этой формулы оценивается следующим образом:

, .

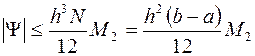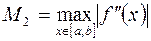Таким образом, формула трапеции имеет, так же как и формула прямоугольников, второй порядок точности, но ее погрешность оценивается величиной в два раза большей.

3. Формула Симпсона. При аппроксимации интеграла (4) заменим функцию 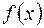параболой, проходящей через точки 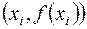, , 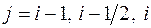т.е. представим приближенно 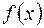в виде

,

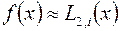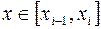
где 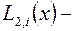интерполяционный многочлен Лагранжа второй степени,

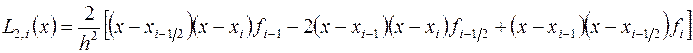(3.13)

Проводя интегрирование, получим (доказать, дом. зад.№3)

, .

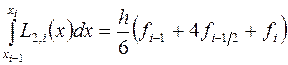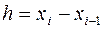Таким образом, приходим к приближенному равенству

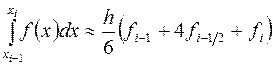, (3.14)

которое называется формулой Симпсона или формулой парабол.

На всем отрезке 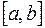формула Симпсона имеет вид

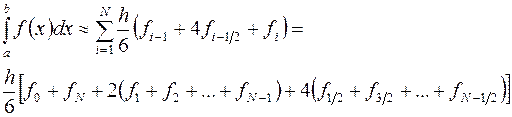. (3.15)

Прежде чем переходить к оценке погрешности формулы (3.14), заметим, что она является точной для любого многочлена третьей степени, т.е. имеет место точное равенство (доказать, дом. зад.№3)

,

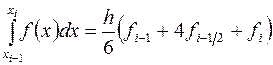если 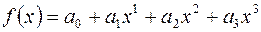. Это утверждение нетрудно проверить непосредственно.

Для оценки погрешности формулы Симпсона воспользуемся интерполяционным многочленом Эрмита. Построим многочлен третьей степени 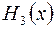, такой, что

, ,

, .

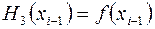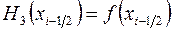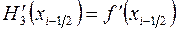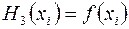Известно (см. лекция 1.3), что такой многочлен существует и единственен. Он построен в явном виде в примере, который там разбирается. Однако нам даже и не потребуется явный вид многочлена 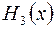. Воспользуемся тем, что формула Симпсона точна для любого многочлена третьей степени, получим

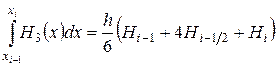. (3.16)

Представим теперь 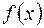в виде

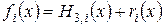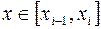, , (3.17)

где 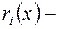погрешность интерполирования многочленом Эрмита 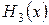. Интегрируя (3.17) и учитывая (3.16), получим

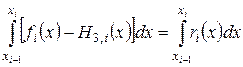. (3.18)

Согласно (2.18) из лекции 1.3 имеем

,

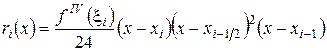поэтому из (3.18) для погрешности 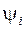из формулы (3.14) получаем оценку

,

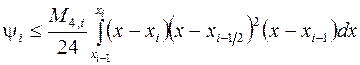где .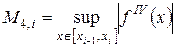

Вычисляя интеграл, приходим окончательно к оценке (доказать, дом. зад.№3)

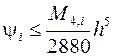. (3.19)

Погрешность составной формулы Симпсона (15) оценивается так:

, , .

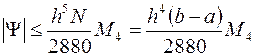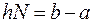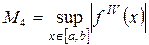Отсюда видно, что формула Симпсона существенно точнее, чем формулы прямоугольников и трапеций.

4 Апостериорная оценка погрешности методом Рунге.
Автоматический выбор шага интегрирования

Величина погрешности численного интегрирования зависит как от шага сетки 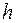, так и от гладкости подынтегральной функции 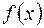. Например, в оценку (3.11) наряду с 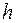, входит величина

,

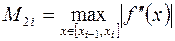которая может сильно меняться от точки к точке и, вообще говоря, заранее неизвестна. Если величина погрешности велика, то ее можно уменьшить путем измельчения сетки на данном отрезке 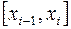. Для этого, прежде всего, надо уметь апостериорно, т.е. после проведения расчета оценивать погрешность.

Апостериорную оценку погрешности можно оценить методом Рунге, который поясним на примере формулы трапеции. Пусть отрезок 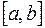разбит на частичные отрезки 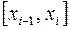, , 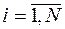, 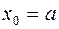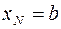с постоянной длиной, что не принципиально. На каждом частичном отрезке применяется формула трапеций

.

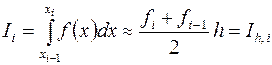Согласно (3.11) имеем

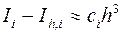, (3.20)

где константа 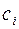зависит от гладкости 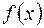и заранее неизвестна. Измельчим на отрезке 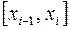сетку в два раза и повторим расчет с шагом 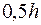, т.е. вычислим сумму

.

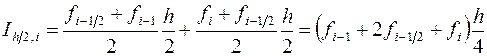Тогда согласно (3.20) будем иметь

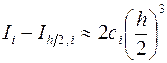. (3.21)

Из соотношений (3.20) и (3.21) можно исключить константу 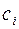и получить оценку погрешности, которая содержит лишь известные величины :

,

.

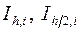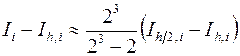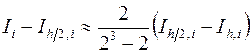Разумеется, метод Рунге можно применять и для оценки погрешности других квадратурных формул. Пусть какая-то квадратурная формула имеет на частичном отрезке порядок точности 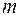, т.е. 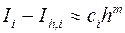. Тогда

,

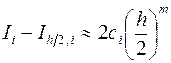откуда получим (доказать, дом. зад.№3)

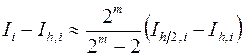, (3.22)

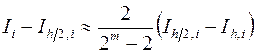. (3.23)

Возможность апостериорно оценивать погрешность позволяет вычислять интеграл (3.1) с заданной точностью 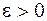путем автоматического выбора шага интегрирования 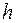. Пусть используется составная квадратурная формула

.

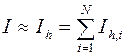Проведем на каждом частичном отрезке 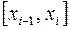все вычисления дважды, один раз ‑ с шагом 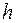и второй раз – с шагом 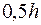и оценим погрешность по правилу Рунге (3.23).

Если для заданного 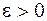будут выполняться неравенства

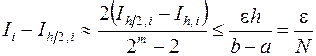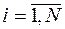, , (3.24)

то получим

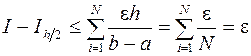или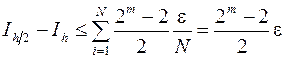

и тогда будет достигнута заданная точность .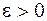

Дата добавления: 2014-01-13