Алгоритмы поиска на графе

Существует много алгоритмов на графах, в основе которых лежит систематический перебор вершин графа, при котором каждая вершина просматривается в точности один раз. Рассмотрим два таких метода поиска в неориентированном графе, которые стали основными методиками проектирования графовых алгоритмов.

Поиск в глубину в графе

Общая идея метода напоминает поиск в лабиринте чудовища Минотавра, описанного в древнегреческом мифе об Ариадне и Тезее. Поиск начинается с некоторой фиксированной вершины v₁. Она помещается в стэк. Затем выбирается произвольная вершина u, смежная с v₁ (если смежных вершин несколько, берется вершина с меньшим номером), и повторяется процесс от вершины u. Предположим, что на очередном шаге выбрана вершина w. Если существует новая (еще непросмотренная) вершина t, смежная с вершиной w, то продолжаем поиск с вершины t. Если же не существует ни одной вершины, смежной с w, то говорят, что вершина w использована до конца, и процесс продолжается с вершины, из которой был переход в вершину w (вершина w удаляется из стэка). Процесс заканчивается, когда происходит возврат в вершину v₁ и новых смежных с v₁ вершин нет.

Идею поиска в глубину можно реализовать с помощью рекурсивной процедуры (массив признаков посещения вершин графа p[1..n] of 0..1 и матрица смежности a[1..n, 1..n] of 0..1 - глобальные):

procedure vg(v: integer);

var u: integer;

begin p[v]:= 1;

for u:= 1 to n do

if (a[v,u] =1) and not p[u] then vg(u)

end;

Очевидно, поиск в глубину в графе просматривает все вершины одной компоненты графа или все его вершины, если он связен. В последнем случае, просмотренные ребра графа образуют остов связного графа, построенный поиском в глубину.

Пример. Применим поиск в глубину к графу, изображенному на рис. 7.1.

Последовательность посещения вершин графа при поиске в глубину такова:

1, 2, 3, 4, 5, 6, 7, возврат в вершину 6, 8. Пройденные ребра образуют остов графа, изображенный на рис. 7.2.

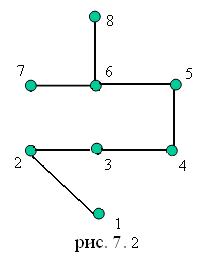
Если G - (n,m)-граф, то нетрудно видеть, что количество операций при поиске в глубину кратно величине n + m. Говорят в таком случае, сложность алгоритма равна O (n+m), или время выполнения алгоритма равно O(n+m).

Таким образом, поиск в глубину очень эффективный метод, однако он строит цепи от начальной вершины до других вершин, не являющиеся кратчайшими, например, длина цепи (1,8) равна 6, хотя в графе есть цепь (1, 4, 6, 8) длины 3.

Поиск в ширину в графе

Поиск в ширину основывается на использовании структуры очередь- чем раньше посещается вершина, тем раньше она удаляется из очереди.

Поиск в ширину начинается с некоторой фиксированной вершины v₁, как и при поиске в глубину. Пройденная вершина помещается в очередь. Далее из очереди удаляется вершина из начала очереди (на первом шаге - v₁), а в конец очереди записываются все новые, смежные с удаляемой, вершины. Удаление из очереди и поиск новых смежных с удаляемой вершин оканчивается, когда очередь станет пустой.

Последовательность посещения вершин графа при поиске в ширину такова:

1, 2, 3, 4, 7, 5, 6, 8. Пройденные ребра образуют остов графа, изображенный на рис. 7.3.

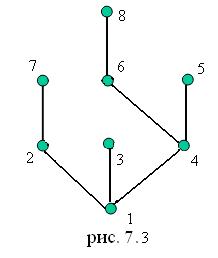
Описание алгоритма поиска в ширину требует построения нескольких процедур работы с очередью (удаление из очереди, добавление в очередь, проверка пустоты очереди), однако цепи от начальной вершины до других вершин графа при поиске в ширину имеют наименьшую длину. На рис. 7.3 видно, что цепь (1, 8) имеет длину 3, являясь кратчайшей.

Дата добавления: 2014-01-11