Джерелом нескінченої потужностіназивають таке джерело, напруга на шинах якого змінюючись з постійною частотою, має незмінну амплітуду і власний опір якого дорівнює нулю

Під простішим трифазним колом розуміють коло із зосередженими параметрами при відсутності в ньому трансформаторних зв”язків, яке живиться від джерела нескінченої потужності.

ПЕРЕХІДНІ ПРОЦЕСИ В ПРОСТІШОМУ ТРИФАЗНОМУ КОЛІ

Лекція 3

Розглянемо перехадні процеси, які виникають в схемі, наведеній на рис. 3.1, післі ввімкнення вимикача В

Напряжение, например, в фазе А изменяется по синусоидальному закону 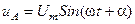. Параметр 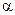представляет собою фазу включения..

Задача полягає у визначенні законів змінення струмів в фазах А, В, С після ввімкнення вимикача В, за яким установлена закоротка.

Після включення вимикача схема розділюється на два незалежні одне від одного кола. Одне з них (ліве з опорами 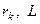) залишається підключеним до джерела напруги, друге уявляє собою короткозамкнений контур ().

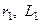Розглянемо спочатку процеси, які протікають в короткозамкненому контурі.

Для кожної фази цієї дільниці справедливий вираз

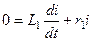. (3.1)

Рішення цього рівняння має вигляд

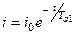. (3.2)

Воно показує, що в цьому короткозамкненому контурі протікає тільки вільний (аперіодичний) струм, який загасає за експоненційним законом з постійною часу

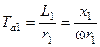, с. (3.3)

Фізично це означає, що струм в короткозамкненому контурі буде підтримуватися на протязі часу, який необхідний для того, щоб енергія магнітного поля, яка накопичена в індуктивності 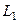, не перетворилася в тепло, виділене на активному опорі 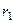. Величина попереднього миттєвого значення струму визначає початкове значення вільного струму в кожній фазі зашунтованої дільниці кола в момент включення вимикача, оскільки в колах з індуктивністю стрибкоподібного змінення струму відбутися не може.

Рассмотрим векторную диаграмму (рис.3.2).

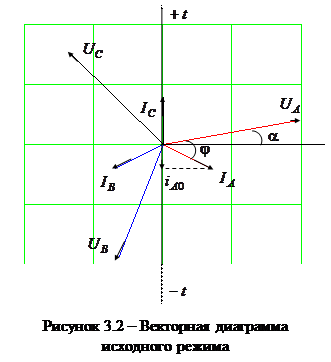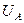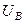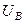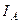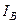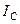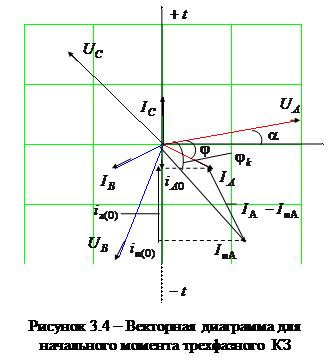
Вращающиеся векторы , , , , , характеризуют предшествующий режим. Вертикаль tt является неподвижной линией времени. Мгновенные значения отдельных величин определяются как проекции на эту линию соответствующих векторов. Момент возникновения КЗ будем фиксировать значением угла 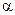, (т.е. фазой включения) между вектором напряжения фазы А и горизонталью.

На рис. 3.3 справа показана векторная диаграмма токов в момент КЗ, а также изменения токов в зашунтированном участке схемы до и после короткого замыкания.

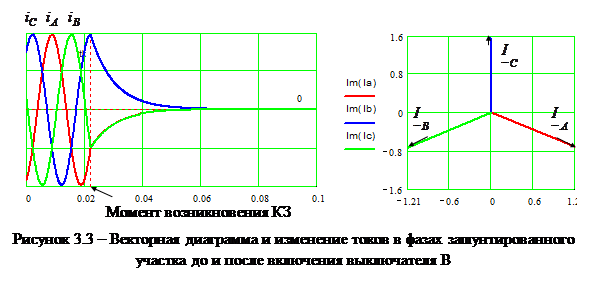
Очевидно, что в общем случае свободные токи в фазах различны, хотя их затухание, разумеется, происходит с одной и той же востоянной времени. В одной из фаз свободный ток может вообще отсутствовать, если в момент КЗ предшествовавший ток в этой фазе проходил через ноль. При этом свободные токи в двух других фазах будут одинаковы по величине, но противоположны по знаку.

Рассмотрим процессы, происходящие в цепи, которая осталась подключенной к источнику питания.

Для фазы А этого участка справедливо следующее уравнение

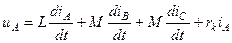. (3.4)

Поскольку, 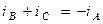, то

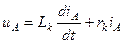, (3.5)

где 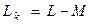- результирующая индуктивность фазы А.

Аналогичные уравнения должны быть записаны и для фаз В и С. Тогда в общем виде для любой фазы участка, подключенного к источнику, можно записать

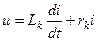. (3.6)

Решение этого уравнения имеет вид , где

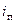- принужденный ток, обусловленный действием приложенного от источника напряжения;

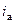- свободный (апериодический) ток.

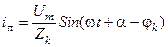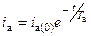; . (3.7)

В (3.7) 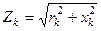- полное сопротивление цепи, оставшейся подключенной к источнику напряжения; 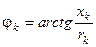- аргумент полного сопротивления этой цепи, или угол сдвига тока от напряжения в этой цепи; 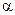- фаза включения, т.е. угол, определяющий значение напряжения в фазе А в момент времени .

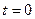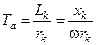. (3.8)

Ток 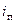представляет периодическую слагающую, которая в рассматриваемых условиях является вынужденным (принужденным) током с постоянной амплитудой 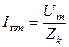. Ток 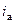- это затухающий по экспоненте свободный апериодический ток. Его начальное значение 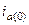определяется из начальных условий в соответствии с первым законом коммутации: ток в индуктивности не может изменяться скачком. Тогда,

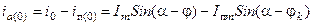, (3.9)

где 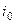- мгновенное значение тока предшествующего режима в момент включения выключателя (цепь: 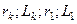); - мгновенное значение принужденного тока в цепи 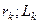, оставшейся подключенной к источнику, в момент включения выключателя.

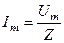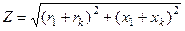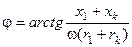; ; . (3.10

Построим векторную диаграмму токов в начальный момент короткого замыкания. Она показана на рис. 3.4. В зависимости от фазы включения 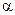меняется начальное значение 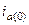от нуля (когда вектор 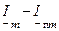параллелен линии времени) до некоторого наибольшего значения, когда этот вектор нормален к ней. Очевидно, что в общем случае все начальные значения свободных токов в фазах разные. Изобразим осциллограмму токов.

На рис.3.5 приведена осциллограмма изменения токов в фазе А.

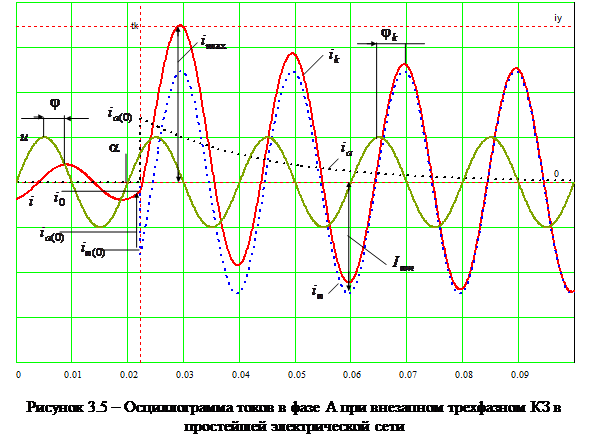Из рис.3.5 видно, что апериодическая составляющая является криволинейной осью симметрии изменения полного тока. Наибольшее мгновенное значение полного тока КЗ 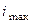зависит от тока предшествующего режима и от фазы включения 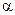. При отсутствии тока исходного режима, величина 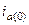может достигать амплитуды периодической принужденной слагающей, если в момент КЗ эта составляющая проходит через свой положительный или отрицательный максимум. Однако максимум апериодической составляющей не предопределяет того, что в этом случае будет максимальным мгновенное значение полного тока КЗ. Этот максимум называют ударным током.

Максимум полного тока (ударный ток) является функцией двух переменных 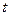и 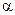и определяется выражением

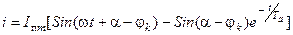. (3.11)

Приравняв нулю частные производные 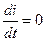и 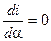и решив совместно эти эти уравнения найдем, что ударный ток наступает при условии 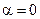. Следовательно, в предварительно разомкнутой цепи с индуктивностью ударный ток при КЗ наступает, если в момент возникновения КЗ мгновенное значение напряжения источника равняется нулю.

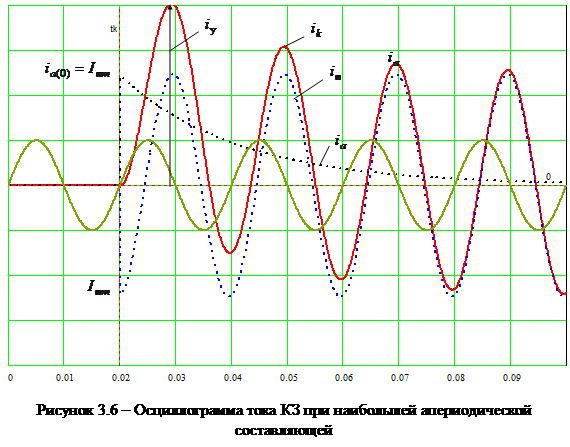На рис.3.6. показана осциллограмма токов в фазе А, когда в момент КЗ апериодическая составляющая имеет наибольшее значение, т.е. принужденный ток в момент повреждения проходит через амплитудное значение.

Для цепей с преобладающей индуктивностью угол , поэтому условие действительные возникновения ударного тока близки к условиям, когда апериодический ток имеет наибольшее значение. Поэтому в практических расчетах значение ударного тока 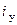, обчно определяют при наибольшем значении апериодической составляющей (рис.3.6). Из рис.3.6 следует, что ударный ток наступает через полпериода промышленной частоты, т.е. через 0,01 с после возникновения КЗ. Таким образом, выражение для расчета ударного тока можно записать в следующем виде:

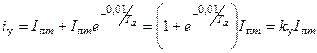, (3.12)

или

,

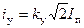где 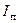- действующее значение принужденного тока.

Ударный коэффициент показывает превышение ударного тока над амплитудой периодической составляющей.

При () .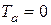

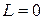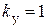При () .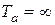

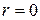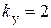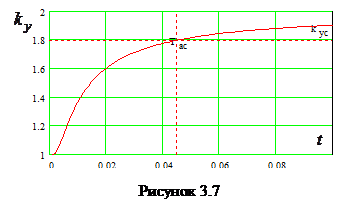
Следовательно, 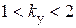. Естественно, чем меньше постоянная времени, тем быстрее затухает апериодическая слагающая и тем соответственно меньше ударный коэффициент. Зависимость ударного коэффициента от постоянной времени затухания приведена на рис. 3.7.

Для высоковольтных систем значение 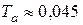с. Это соответствует величине ударного коэффициента, равного 1.8. Следует обратить внимание на то, что апериодические составляющие токов в фазах различны. Поэтому определение трехфазного короткого замыкания как симметричного, строго говоря, справедливо к периодическим слагающим токов.

Дата добавления: 2014-01-11