Словесное описание ФАЛ

СПОСОБЫ ЗАДАНИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ

Рис.1.1 Обобщенная схема логического устройства

Рассмотрим некоторое логическое устройство, на входе которого присутствует некоторый n-разрядный двоичный код х_{n- 1} ... х₁х_о , а на выходе соответственно m-разрядный двоичный код z_m-1... z₁z₀ (рис. 1.1). Для того чтобы описать поведение этой схемы, необходимо определить зависимость каждой из т выходных переменных z _i от входного двоичного кода х_{n- 1} ... х₁х_о.

Зависимость выходных переменных z_i, выраженная через совокупность входных переменных х_{n- 1} ... х₁х_о с помощью операций алгебры логики, называется функцией алгебры логики (ФАЛ). Иногда данную зависимость также называют переключательной функцией. Задать ФАЛ - это значит определить значения z _i для всех возможных комбинаций переменных х_{n- 1} ... х₁х_о. Очевидно, что для n-разрядного двоичного кода х_{n- 1} ... х₁х_о, существует 2ⁿ различных значений z _i.

Функция называется полностью определенной, если заданы 2ⁿ ее значений. Если часть значений функции не задана, то она называется частично определенной или недоопределенной.

Иногда известно, что по условиям работы устройства появление некоторых входных кодов невозможно, и поэтому значения ФАЛ на этих кодах не задаются. При этом возникают так называемые факультативные или необязательные значения функции, которые могут задаваться произвольными. Входные коды, для которых ФАЛ имеет факультативные значения, называются запрещенными.

Устройства, поведение которых описывается при помощи ФАЛ, называют логическими.

Для описания ФАЛ могут быть использованы различные способы. Основными из них являются описание функции в словесной форме, в виде таблиц истинности, алгебраических выражений, последовательностей десятичных чисел, а также кубических комплексов.

Проиллюстрируем словесное описание ФАЛ на примере.

Пример 1.5. Логическая функция трех переменных равна единице, если хотя бы две входные переменные равны единице (рис.1.1).

Данный вид описания наиболее часто применяется для первоначального, исходного описания поведения логического устройства.

Описание ФАЛ в виде таблицы истинности

Таблица, содержащая все возможные комбинации входных переменных х_{n- 1} ... х₁х_о и соответствующие им значения выходных переменных z _i; называется таблицей истинности или комбинационной таблицей. В общем случае таблица истинности содержит 2ⁿ строк и т + n столбцов. Существуют таблицы истинности переменных и функций.

Таблица истинности переменных

Проиллюстрируем построение таблицы истинности на примере.

Пример 1.6. Составить таблицу истинности (табл. 1.4) для ФАЛ из примера 1.5.

Р е ш е н и е. Данная таблица имеет по четыре столбца и строки.

Таблица 1.4

Таблица истинности для трех переменных

Таблица истинности функций

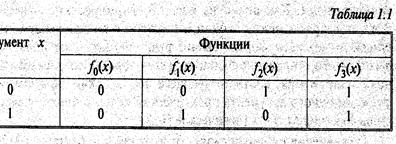Таблица истинности для функций одного аргумента представлена в табл.1.5

Аргумент x

Табл.1.5

Если число аргументов функции равно n, то число различных сочетаний (наборов) значений

_n

аргументов составляет 2ⁿ, а число различных функций и аргументов 2². Так, при n = 2 число наборов значений аргументов равно 2² = 4, число функций 2⁴ = 16. Таблица истинности функций двух аргументов представлена табл. 1.6.

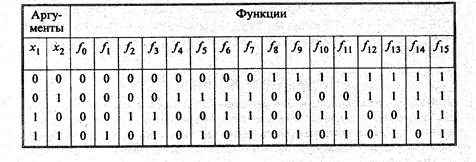
Табл. 1.6

В табл. 1.7 приведен перечень логических операций, используемых при записи логических выражений.

Таблица 1.7

Таблица логических операций

Обозначение логических операций	Таблица истинности	Как читается	Название операции
x 1
Основное	Дополни-тельные	x2
x1 x2	x1 x2 x1 Ù x2 x1 & x2	x1 · x2					x1 и x2	Конъюнкция; логическое И; логическое произведение
x1 Ú x2	x1 + x2	x1 Ú x2					x1 или x2	Дизъюнкция; логическое ИЛИ; логическаясумма
x1 ® x2	x1 É x2	x1 ® x2					если x1 ,то x2; x1 влечет x2; x1 имплицирует x2	Импликация
x1 ~ x2	x1 º x2 x1 «x2	x1 ~ x2					x1 эквивалентно x2	Эквивалентность; равнозначность
x1 Å x2	x1 É x2	x1 Å x2					либо x1, либо x2; x1 неэквива­лентно x2	Сумма по модулю; неравнозначность; исключающее ИЛИ
x1 r x2	x1 ® x2 x1 É x2	x1 r x2					x1 запрет по x2; x1, но не x2	Запрет; отрицание импликации
x1 ï x2	—	x1 ï x					x1 и x2 несовместны	Логическое И-НЕ; элемент (штрих) Шеффера; отрицание конъюнкции
x1 ¯ x2	—	x1 ¯ x2					ни x1, ни x2	Логическое ИЛИ-НЕ; стрелка Пирса; функция Вебба; отрицание дизъюнкции
х	ù х	х			не х	Логическое НЕ; инверсия; логическое отрицание
х

Таблицы истинности дают полную информацию об устройстве и широко используются для их описания. Для этого входные переменные располагают в таблице истинности так, что их последовательность образует двоичное число x₁x₀ ,соответствующееномерунабора i в десятичной системе счисления (поэтому колонку с номерами наборов часто в таблицу не включают).

Составим таблицу (табл.1.8) полного набора логических функций для устройства с двумя входами и 16-ю выходами. Каждая функция Y_n является результатом выполнения одной из 16-ти операций над входными переменными x₁ и x₀ на всех i –ых наборах.

Таблица 1.8

Табл. истинности		Название операции (функции)
i	0	1	2	3	Запись операции (функции)
x1	0	0	1	1
x0	0	1	0	1
yo	0	0	0	0	0	Постоянный 0
Y1	0	0	0	1	x1· x0	Конъюнкция (И)
Y2	0	0	1	0	x1 ® x0 = x1 x0	Запрет по x0
Y3	0	0	1	1	x1	Переменная x1
Y4	0	1	0	0	x0 ® x1 = x1 x0	Запрет по x1
Y5	0	1	0	1	x0	Переменная x0
Y6	0	1	1	0	x1 Å x0 = x1 x0 + x1 x0	Неравнозначность
Y7	0	1	1	1	x1 + x0	Дизъюнкция (ИЛИ)
Y8	1	0	0	0	x1 ¯ x2 = x1 + x0	Стрелка Пирса (ИЛИ-НЕ)
Y9	1	0	0	1	x1 ~ x0 = x1 x0 + x1 x0	Равнозначность
Y10	1	0	1	0	x0	Инверсия (НЕ) x0
Y11	1	0	1	1	x0 ® x1 = x1 + x0	Импликация от x0 к x1
Y12	1	1	0	0	x1	Инверсия (НЕ) x1
Y13	1	1	0	1	x1 ® x0 = x1 + x0	Импликация от x1 к x0
Y14	1	1	1	0	x1 ï x0 = x1 x0	Штрих Шеффера (И-НЕ)
Y15	1	1	1	1	1	Постоянная 1

Дата добавления: 2014-01-14