Линейный двусвязный список

Begin

Отсортированный список.

Слияние двух отсортированных списков в третий

Begin

Begin

Begin

Begin

New(s); { создали новый узел, ссылка на него в s }

s^.i:= a; { a à в новый узел }

t:= h; {встали на начало списка}

p:= Nil; { p - указатель на предыдущий узел}

{ Цикл поиска и вставки узла в надлежащее место списка }

While t < > Nil Do { пока не достигнут конец списка }

If t^.i > a { поиск места вставки }

Then { если место вставки найдено }

If p = Nil { и если р не успел измениться,то}

Then Begin s^.L:= h; h:= s; Exit; End { вставка в начало списка }

Else Begin s^.L:= t; p^.L:= s; Exit; End { вставка в середину списка }

Else Begin p:= t; t:= t^.L; End; { место вставки не найдено и переход к след. узлу }

{ конец цикла While }

If h = Nil Then Begin h:= s; s^.L:= Nil; End { вставка в пустой список }

Else Begin s^.L:= Nil; p^.L:= s; End; { вставка в конец списка }

End;

Процедуру InsList удобно использовать для создания отсортированного списка. Действительно, начав с пустого списка, каждое очередное значение а_i вставляется и коммутируется в надлежащее в ему место в списке.

Procedure CreateSortList (Var h:u; k:integer); {k – длина списка}

Var j:Integer;

h:= Nil;

For j:= 1 To k Do InsList (h, Random(50));

End;

Для того, чтобы упростить алгоритмы операций вставки и удаления и свести их к однотипным операциям часто список снабжают дополнительным узлом, например, в начале списка - его называют заглавным узлом (звеном). В информационном поле заглавного узла может помещаться, например, количество узлов в списке или некоторая другая информация. Ниже приведены процедуры удаления и вставки, по ним видно - на сколько упрощается логика алгоритмов этих операций со списком.

Procedure DelListZ(h:u; a:Integer);

Var p,t:u;

p:=h; t:=h^.L;

While t <> Nil Do

If t^.i = a Then Begin p^.L:= t^.L; Dispose(t); Exit; End

Else Begin p:= t; t:= t^.L; End;

Writeln('такого элемента нет');

End;

Procedure InsListZ(h:u; a:Integer);

Var p, t, s:u;

New(s); s^.i:= a;

p:=h; t:=h^.L;

While (t<>Nil) And (t^.i <= a) Do

Begin p:= t; t:= t^.L; End;

p^.L:= s; s^.L:= t;

End;

Пусть заданы два непустых и отсортированных по возрастанию списка h1 и h2. Получить объединенный отсортированный список за счет перекоммутации ссылок между узлами списков. Голова объединенного списка будет h1.

Procedure AddList (Var h1, h2:u);

Var p, t1, t2:u;

If h1^.i > h2^.i { добиваемся, чтобы h1 указывал на первый элемент с

Then Begin t1:=h1; h1:=h2; h2:=t1; End; меньшим значением}

t1:= h1; p:=Nil; t2:= h2;

Repeat {цикл объединения списков}

While (t1< > Nil) And (t1^.i <= t2^.i) Do Begin

p:=t1; t1:= t1^.L; { продвижение по текущему списку пока не

End; нужна перекоммутация }

p1^.L:= t2; t2:= t1; t1:= p^.L; { коммутация двух узлов из разных списков }

Until t2 = Nil; { если достигли конца одного из списков – задача выполнена }

End;

Рассмотренные ЛС являются структурами с последовательным доступом. Еще их называют односвязными, поскольку связи между узлами однонаправлены и просматривать элементы списка можно только от начала к концу. В некоторых практических задачах более эффективной структурой для представления данных яв­ляются двусвязные ЛС, где каждый элемент (узел) содержит ссылку не только на следующий, но и на предыдущий элементы. Обычно их еще называют R – правой ссылкой и L – левой ссылкой. В таких ЛС можно продвигаться как в пря­мом, так и обратном направле­ниях. Далее приведены соответст­вующие основные объявления и процедуры демонстрирующие ра­боту с двусвязными ЛС.

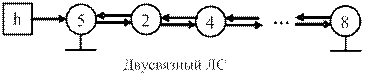
Дата добавления: 2014-01-11