Из (3) имеем

Закон сохранения энергии имеет вид

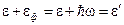(1)

Закон сохранения импульса

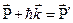(2)

Выражая энергию через импульс, получаем:

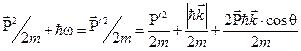(3)

где 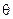- угол между 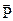и

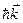
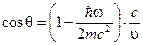(4)

В оптическом диапазоне 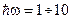Эв, 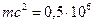- Эв, т.е. 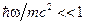и поскольку 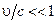получаем, что 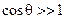, что невозможно.

Таким образом, свободный электрон не может ни поглощать энергию из электромагнитной волны, ни излучать свою энергию в эту волну - вот какой вывод следует из законов сохранения, причем он справедлив, как можно легко показать, и в релятивистском случае, когда .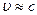

Какой же процесс может осуществляться при взаимодействии свободного электрона с электромагнитным полем? Это процесс рассеяния фотоном электрона (или наоборот), изображен на рис. 2 который характеризуется сравнительно низкой эффективностью передачи энергии от поля электрону, даже в случае лобового столкновения .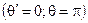

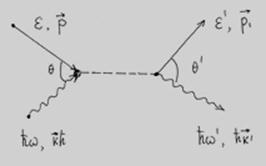
Запишем законы сохранения.

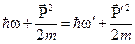
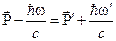(5)

Рис.2

Вводя 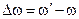, (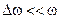) для

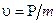
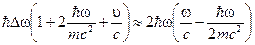(6)

С учетом нерелятивистского фактора ,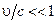

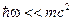
получаем

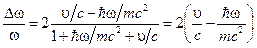(7)

В этом выражении, (которое является нерелятивистским аналогом формулы, описывающей изменение частоты фотона при эффекте Комптона) содержатся одновременно и эффект "отдачи" (передачи части энергии фотона 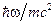- электрону), и эффект Доплера - изменение частоты рассеянного фотона .

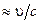Оценка изменения энергии электрона при однократном "лобовом" столкновении с фотоном 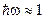Эв из (7) для начальной скорости электрона с энергией 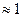Эв

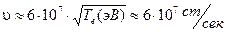даст

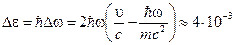эВ (8)

1.2 Классическое рассмотрение процесса взаимодействия свободного электрона с внешним электромагнитным полем, которое описывается уравнением Максвелла, приводит к аналогичному результату.

Если имеется монохроматическая волна

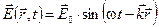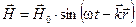, , то

уравнение движения свободного электрона имеет вид

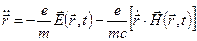(9)

При условии, что смещение электрона в поле волны мало, 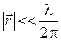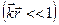, будем учитывать только временную зависимость поля и, кроме того, пренебрегаем силой Лоренца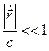

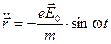(10)

Решение (10) имеет вид:

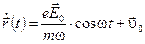(11)

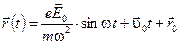(12)

Приближение свободных колебаний имеет смысл, если частота колебаний столь велика или столкновения столь редки, что за время между столкновениями электрон успевает совершить много осцилляций в переменном электрическом поле.

В общем случае это условие записывается в ви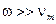де , где 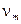- эффективная частота столкновений.

Энергия колебаний электрона в поле монохроматической волны, усредненная за период

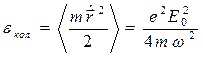(13)

Выразим (13) через интенсивность волны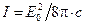, тогда

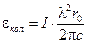(14)

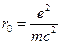- классический радиус электрона.

Энергия 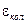приобретается электроном на стадии "включения" поля, тогда как в установившемся режиме поле не совершает работы.

Вычислим среднюю за период, поглощаемую электроном мощность:

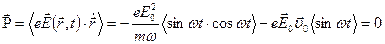(15)

Учет радиационного "трения" электрона, пропорционального 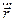, приводит, как известно, к явлению упругого (томсоновского) рассеяния света с полной мощностью излучения в телесный угол 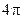радиан:

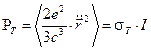(16)

где: 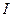- интенсивность света,

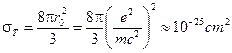(17)

- сечение томсоновского рассеяния.

Таким образом, свободный электрон в классической картине взаимодействия с полем, на этапе включения поля приобретает энергию 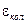, а в установившемся режиме рассеивает небольшую долю падающей на него мощности в виде томсоновского рассеивания.

2. Влияние столкновений.

Столкновения нарушают строго гармонический режим колебаний электрона, "сбивая" их фазу. Чтобы учесть это обстоятельство, включим в уравнение движения электрона эффективную скорость потери импульса, связанную с действием столкновений.

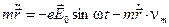(18)

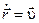
Решение этих уравнений имеет вид:

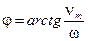, (19)

Амплитуда смещения электрона и его скорости в 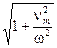раз меньше, чем для свободных колебаний. Сама величина 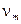определяется скоростью хаотического движения, которая в разрядах гораздо больше колебательной 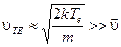. Смещение сдвинуто по фазе относительно поля. Фазовый сдвиг возрастает от 0 до 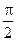при возрастании относительной роли столкновений от 0 до .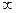

Колебательное смещение и скорость (19) всегда можно представить в виде двух составляющих, одна из которых пропорциональна самой величине поля 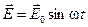, а другая - скорости его изменения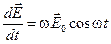

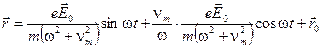
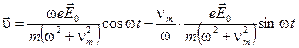(20)

В пределе 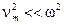формулы (19, 20) приближаются к формулам (11, 12) для свободных колебаний.

В пределе 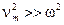колебательная скорость становится равной

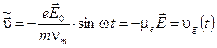(21)

и совпадает в каждый момент времени со скоростью дрейфа. Электрон ведет себя, как в постоянном поле, следуя его медленным изменениям.

Смещение электрона 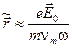имеет амплитуду, которая в 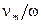раз меньше амплитуды свободных колебаний в том же поле.

3. Энергия электронов.

При наличии столкновений осуществляется систематическая передача энергии электронам, сопровождаемая диссипацией энергии поля. Средняя за период работа поля над электроном в 1 сек (мощность) равна

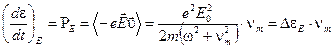(22)

и определяется той составляющей колебательной скорости, которая осциллирует в фазе с величиной поля и которая пропорциональна 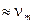. В одном эффективном столкновении электрон приобретает в среднем энергию

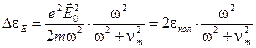(23)

В пределе редких столкновений

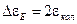(24)

Таким образом, в промежутке между столкновениями электрон под действием электрического поля приобретает некую кинетическую энергию, в среднем порядка 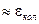. Если за период между столкновениями электрон успевает совершить много колебаний, то эта величина 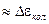(13, 14). Эта приобретенная с момента предыдущего столкновения порция энергии переходит в энергию поступательного, хаотического движения.

Электроны не только приобретают энергию от поля, но и передают ее при столкновении с тяжелыми частицами, ионами, атомами и молекулами. Если при каждом столкновении электрон теряет долю от своей энергии 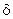, то

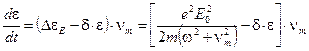(25)

В стационарных условиях 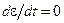устанавливается средняя энергия

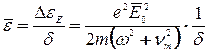(26)

где: 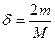, 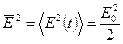- среднеквадратичное поле.

На больших частотах 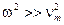средняя энергия электронов при 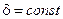; 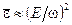. Именно по этой причине для пробоя газа на оптических частотах нужны большие поля 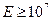В/см, которые реализуются в мощных лазерных пучках.

Следует отметить, что вследствие сохранения суммарного импульса взаимодействующих частиц, полный импульс системы одинаковых частиц 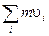осциллирует как 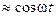, будучи сдвинутым по фазе относительно поля на .

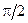Суммарная энергия частиц при упругих столкновениях также сохраняется. Найдем скорость изменения энергии газа, состоящего из одних электронов.

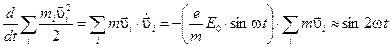(27)

Дата добавления: 2014-01-14