Построение дерева Пифагора

Следующим примером может быть известное "Пифагорово дерево". Оно часто изображается так, как показано на рис. 3.2. Каждый из прямоугольных треугольников в этом дереве имеет внутренний угол, равный 45°.

Рис. 3.2 «Пифагорово дерево», регулярная версия

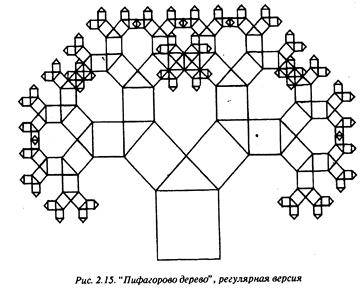
Опять воспользуемся генератором случайных чисел для создания более общей программы, которая может сформировать не только рис. 3.2, но также генерировать и менее регулярные деревья. Углы, задаваемые равными 45° для рис. 3.2, в общем случае будут задаваться случайным образом в пределах между (45 - delta) ° и (45 + delta) °, где значение delta задается в качестве входного параметра вместе с параметром n, определяющим глубину рекурсии. Регулярная версия, изображенная на рис. 3.2, получается при задании delta = 0 и n = 7. На рисунке параметр п определяет количество треугольников на пути от корня до листьев дерева. Сердцевиной программы будет рекурсивная функция square_and_triangle ("квадрат и треугольник") с параметром n, определяющим глубину рекурсии, в качестве первого аргумента. Если значение параметра n больше нуля, то задачей функции square_and_triangle, как это определяется названием, будет вычертить квадрат и над ним треугольник, а затем еще дважды обратиться к самой себе с соответствующими новыми аргументами, первый из которых задается равным n-1. Размер и положение квадрата полностью определяются четырьмя параметрами: X0,Y0, а и j (см. рис. 3.3). Для вычерчивания треугольника необходимо знать угол a. Этот угол, выраженный в градусах, равен 45+deviation, где deviation равно одному из целых чисел ряда -delta, -delta+I,..., delta, выбираемому случайным образом. На рис. 3.3 необходимые точки пронумерованы последовательными числами 0,1,2,3,4. Координаты X0, Y0 точки О задаются в обращении к функции. Для вычисления остальных точек вначале рассмотрим более простую ситуацию при j = 0, то есть когда сторона 0 1 квадрата занимает горизонтальное положение.

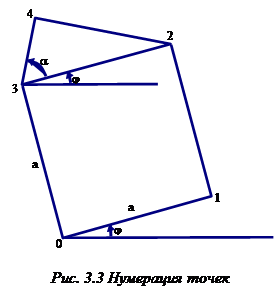В этом положении координаты точек определить очень просто. Они записываются в массивах х и у. Затем вся конструкция поворачивается вокруг точки О на угол j. Результат поворота записывается в массивах хх и уу.

/* PYTH_TREE: Вариант дерева Пифагора */

#include "math.h"

#include "stdlib.h"

#include "time.h"

#define pi 3.1415927

#include "stdio.h"

FILE *fp;

int delta;

long int seed;

struct {float xx; float yy; int ii;} s;

void pfopen(){ fp=fopen("scratch", "wb"); }

void pmove(float x,float y)

{ s.xx=x; s.yy=y; s.ii=0; /* 0 = pen up */ /* 0 = перо поднято */

fwrite(&s, sizeof s, 1, fp);

}

void pdraw(float x,float y)

{ s.xx=x; s.yy=y; s.ii=1; /* 1 = pen down */ /* 1 = перо опущено */

fwrite(&s, sizeof s, 1, fp);

}

void pfclose(){ fclose(fp); }

void square_and_triangle(int n,float x0,float y0, float a, float phi)

{ float x[5], y[5], xx[5], yy[5], cphi, sphi, c1, c2, b, c,

alpha, calpha, salpha;

int i, deviation; /* phi and alpha in radians */

/* delta in degrees */

if(n==0) return; /* углы phi и alpha в радианах */

/* угол delta в градусах */

deviation=rand()%(2*delta+1)-delta;

alpha=(45+deviation)*pi/180.0;

x[0]=x[3]=x0; x[1]=x[2]=x0+a;

y[0]=y[1]=y0; y[2]=y[3]=y0+a;

calpha=cos(alpha); salpha=sin(alpha);

c=a*calpha; b=a*salpha;

x[4]=x[3]+c*calpha;

y[4]=y[3]+c*salpha;

/* Rotation about (x0, y0) through angle phi; */

/* Поворот вокруг точки (x0, y0) на угол phi;*/

cphi=cos(phi); sphi=sin(phi);

c1=x0-x0*cphi+y0*sphi;

c2=y0-x0*sphi-y0*cphi;

for (i=0; i<5; i++)

{ xx[i]=x[i]*cphi-y[i]*sphi+c1;

yy[i]=x[i]*sphi+y[i]*cphi+c2;

}

pmove(xx[3], yy[3]);

for (i=0; i<5; i++) pdraw(xx[i],yy[i]);

pdraw(xx[2], yy[2]);

square_and_triangle(n-1, xx[3], yy[3], c, phi+alpha);

square_and_triangle(n-1, xx[4], yy[4], b, phi+alpha-0.5*pi);

}

void main()

{ int n;

pfopen(); time(&seed); srand((int)seed);

printf (" Задайте угол delta в градусах (0 < delta < 45) ");

scanf("%d", &delta);

printf(" Задайте глубину рекурсии n "); scanf("%d", &n);

square_and_triangle(n, 0.0, 0.0, 1.0, 0.0);

pfclose();

}

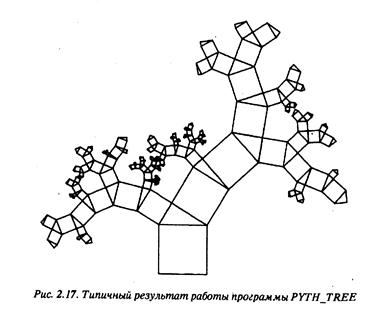
Эта программа формирует файл SCRATCH, который должен быть обработан программой G ENPLOT из лекции 2. Графический результат работы программы для delta = 30 и п = 7 показан на рис. 3.4.

Рис 3.4 Типичный результат работы программы PYTH_TREE

Дата добавления: 2014-01-14