Минимизация на отрезке

Пусть функция f (x) задана на 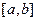аналитически. Тогда можно поставить задачу о минимизации остаточного члена интерполирования на всем отрезке 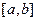. Т.е. ставим задачу, как выбрать на отрезке 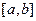точки интерполирования 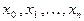, чтобы величина 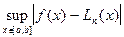была наименьшей. Это значит, что в качестве узлов интерполирования нужно взять точки 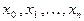, являющиеся корнями многочлена 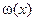степени 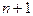, который на промежутке 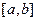принимает наименьшее по абсолютной величине значение среди всех многочленов степени 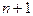со старшим коэффициентом 1. Рассмотрим промежуток 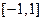. На этом промежутке можно положить 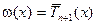, где 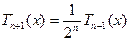. Следовательно, на промежутке 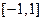узлами интерполирования будут корни полинома Чебышева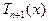

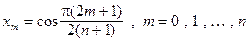(4.15)

Максимальное по модулю значение многочлен 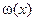будет принимать в точках, являющихся точками экстремум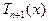а на . Это будут точки

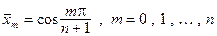+1, причем .

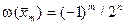Построим по узлам (5.2) интерполяционный многочлен Лагранжа 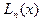. Тогда

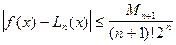(4.16)

где М _n+1 — постоянная, ограничивающая сверху величину .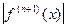

Если нам нужно произвести интерполирование на произвольном промежутке , то произведем замену

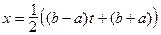
Отсюда

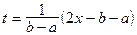
Корни многочлена 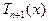перейдут в

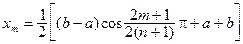(4.17)

Многочленом, наименее уклоняющимся от 0 на будет многочлен

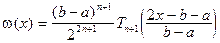
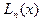Если на взять узлы интерполирования x_m из (4.17) и построить по ним интерполяционный многочлен Лагранжа , то

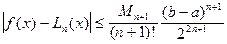(4.18)

Дата добавления: 2014-01-14