Основные понятия о устойчивости АСР

Система всегда подвергается действия внешних возмущающих воздействий. Эти возмущения в некоторые промежутки времени могут стремиться вывести систему из состояния равновесия. Если система устойчива, то она противостоит этим внешним воздействиям, а будучи выведенной из состояния равновесия с определенной точностью возвращается к нему. Если система неустойчива, то она не возвращается в состояние равновесия, а удаляется от него или совершает вокруг него недопустимо большие колебания.

Условие устойчивости – система будет устойчивой, если из возмущенного состояния равновесия она перейдет в некоторую конечную область, окружающую невозмущенное состояние равновесия.

Пример, демонстрирующий устойчивость системы, - перемещение шара по поверхности определенного профиля. Возмущением будет перемещение шара относительно первоначального состояния равновесия и анализ самостоятельного движения шара относительно профиля.

1. Устойчивое состояние системы «шар-поверхность» - состояние, которое остается устойчивым при любых возмущениях.

Шар переведенный из положения А в положение В, последний после ряда колебаний вернется к первоначальному состоянию равновесия.

2. Неустойчивое состояние – состояние системы, при котором любое отклонение от положения равновесия вызовет силу, которая будет стремиться еще дальше увести шар от состояния равновесия.

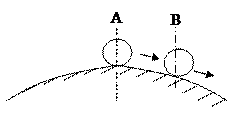Шар переведенный из положения А в положение В, последний чего сила тяжести будет все более увлекать шар от состояния равновесия А.

3. Состояние равновесия устойчивое в малом – состояние, которое остается устойчивым до тех пор, пока отклонение не выйдет за допустимую границу.

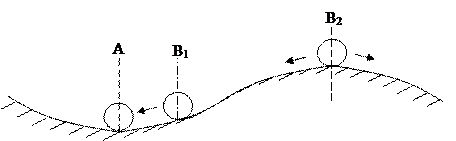Шар, переведенный в положение В₁, самостоятельно вернется в состояние равновесия.

Шар, переведенный в состояние В₂, может как вернуться в состояние равновесия, так и перейти в неустойчивое состояние.

4. Безразличное состояние – состоине, которое отклтикается на возмущение мгновенным переходом к новому состоянию равновесия.

В теории управления за устойчивое состояние часто берется не состояние равновесия, а какое-либо движение с заданной заранее траекторией.

Методов исследования устойчивости системы регулирования разработано много. Рассмотрим классический метод оценки устойчивости системы, основанный на теореме А.М. Ляпунова.

Линейные управления реальных автоматических систем получаются всегда в результате той или иной линеаризации, т.е. в результате отбрасывания членов, содержащих вторые и высшие степени, а также произведения отклонений переменных и их производных. Возникает вопрос: Насколько влияют отброшенные члены на устойчивость систем? Ляпунов доказал ряд оригинальных теорем и предложил ряд методов для исследования устойчивости динамических линеаризованных систем в различных трудных для анализа случаях.

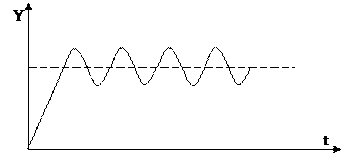
Оценки берутся из анализа характеристического уравнения системы:

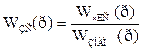
Характеристическое уравнение: .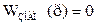

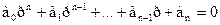
Решение данного уравнения – это корни характеристического уравнения, которые принимают n алгебраических переменных (р_i = a±bi). Оценку устойчивости можно сделать по анализу полученных корней.

1) Если вещественные части всех корней характеристического уравнения - отрицательны, то система регулирования устойчива. Т.е. никакая добавка в виде членов или из произведений не может «испортить» устойчивость системы.

" $ a < 0 Þ АСР устойчива

Отклонение регулируемой величины приходит к установившемуся значению с затухающими гармоническими колебаниями.

2) Если среди корней характеристического уравнения имеется хотя бы один корень с положительной вещественной частью, то система неустойчива. Т.е. никакая добавка в виде членов второй или высшей степеней переменной не может придать устойчивость системе.

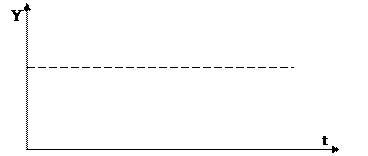$ хотя бы один a_i > 0 Þ АСР неустойчива

Отклонение регулируемой величины совершает колебания с неограниченно возрастающей амплитудой.

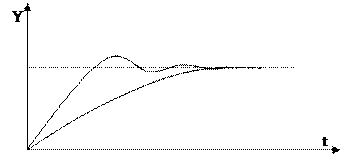
3) Для линейной системы равенство нулю вещественной части хотя бы одного корня характеристического уравнения дает границу устойчивости. По линейным уравлениям нельзя судить что происходит на границе устойчивости, поэтому к этому режиму при работе стараются не приближаться.

$ хотя бы один a_i = 0 Þ АСР на границе устойчивости

Автоколебания

Знаки вещественной части корней можно найти путем непосредственного решения характеристического уравнения. Уравнение третей степени решается аналитически чрезвычайно сложно. Уравнения более высоких степеней вообще не имеют аналитического решения и могут быть решены лишь приближенно.

Для облегчения оценки знака вещественной части корня используются специальные критерии устойчивости.

Критерием устойчивости называется косвенный метод определения знаков вещественной части корней характеристического уравнения, не требующий решения этого уравнения.

Дата добавления: 2014-01-14