Для системы четвертого порядка

.

Критерий устойчивости Гурвица

Приведем теперь критерий устойчивости Гурвица без доказательства.

Для устойчивости линейной системы n- ого порядка необходимо и достаточно, чтобы были положительными n главных определителей матрицы Гурвица, составленной по коэффициентам характеристического уравнения данной системы:

В первой строке матрицы пишутся коэффициенты с нечетными индексами, во второй – с четными. Концы строк заполняются нулями, так чтобы матрица имела n столбцов, где n – порядок уравнения системы. Третья и четвертая строки получаются сдвигом первых двух на одно место вправо и т. д.

Указанные главные определители называются определителями Гурвица и имеют вид:

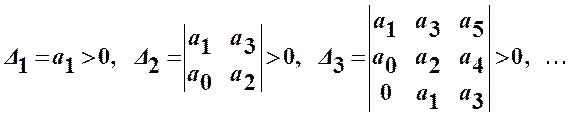
Последний определитель Гурвица, как видно из приведенной выше матрицы, равен D _n =D _{n -1}× a_n, Поэтому его положительность сводится при D _{n -1}>0 к условию a_n >0.

С помощью критерия Гурвица удобно проверять устойчивость линейных до четвертого порядка включительно.

Для систем первого и второго порядка критерий Гурвица сводится просто к положительности коэффициентов a ₀, a ₁, a ₂.

Для системы третьего порядка характеристическое уравнение имеет вид

,

а условие устойчивости по Гурвицу будет D _{n -1}= D₂= a ₁ a ₂ – a ₀ a ₃>0 (n =3), причем остальные неравенства сводятся к требованию положительности коэффициентов a ₀, a ₁, a ₂, a ₃.

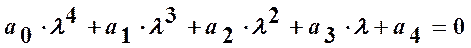
условием устойчивости по Гурвицу будет положительность всех коэффициентов характеристического уравнения a ₀, a ₁, a ₂, a ₃, a ₄ и выполнение неравенства

.

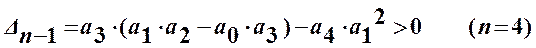Найдем границы устойчивости.

Апериодическая граница устойчивости (нулевой корень) будет в том случае, когда a_n =0, по при условии положительности всех определителей Гурвица (кроме последнего).

Колебательная граница устойчивости (пара чисто мнимых корней в характеристическом уравнении) появляется при D _{n -1}=0, если при этом все остальные определители Гурвица положительны.

Пример. Передаточная функция разомкнутой цепи системы имеет вид:

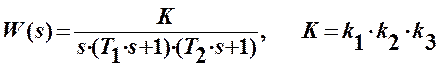
Характеристическое уравнение замкнутой системы будет

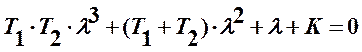
Коэффициенты его положительны. Условие устойчивости по критерию Гурвица получит вид

, .

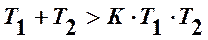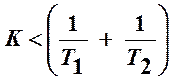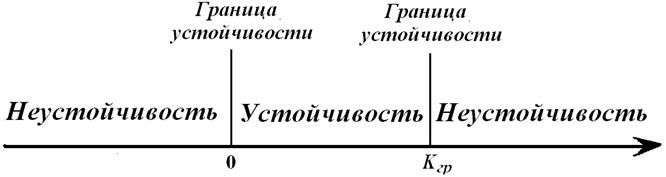
Границы устойчивости:

1) a_n =0, K =0; 2) D _{n -1}=0, K_гр =1/ T ₁+1/ T ₂.

Эти две границы устойчивости можно изобразить графически в пространстве параметра K и найти области устойчивости системы.

Пространство параметров здесь одна прямая линия, а границы устойчивости – точки на ней: K =0 и K = K_гр. Область устойчивости лежит между этими точками.

Дата добавления: 2014-01-14