Лекція 6. Во всех случаях, когда важно получить требуемое качество движения второй массы, а также при регулировании ее координат

Во всех случаях, когда важно получить требуемое качество движения второй массы, а также при регулировании ее координат, пренебрегать влиянием упругостей механических связей нельзя.

В реальных системах присутствуют диссипативные силы, которые оказывают демпфирующее воздействие на колебательную систему (например, внутренние силы вязкого трения) Но это демпфирование в большинстве случаев невелико. Оно существенно не сказывается на частотных характеристиках, однако ограничивает резонансные пики конечными значениями и несколько сглаживают фазочастотные характеристики.

Нетрудно установить, что частотные характеристики абсолютно упругой системы, приводимой к одномассовой, совпадают во всем диапазоне с частотными характеристиками идеального интегрирующего звена, а структурная схема принимает вид

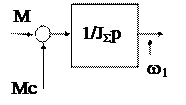Механические переходные процессы

Изменение управляющего или возмущающих воздействий вызывают в механической подсистеме переходные процессы, называемые механическими переходными процессами.

Рассматривая одномассовую систему, движение которой описывается дифференциальным уравнением первого порядка

J_S dw/dt= M- M_c,

где J_S = J₁+J₂ и M_c= M_c1 + M_c2,

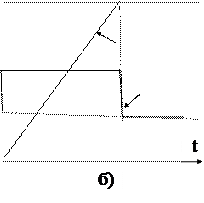
легко установить, что при постоянстве статического момента сопро-тивления закон изменения скорости в переходном процессе определяется характером изменения во времени управляющего момента. Так для получения экспоненциальной кривой скорости при пуске необходимо обеспечить экспоненциальную зависимость момента от времени. Для получения равномерно ускоренного изменения скорости необходимо формировать прямоугольный закон изменения момента двигателя во времени (см. рис. 6.4,а,б).

  w_кон M, w   w(t)     M(t) Mc  

w_кон M, w   w(t)     M(t) Mc        

		а)

Если известен характер изменения момента двигателя и приведенного момента нагрузки с помощью указанного уравнения можно установить характер изменения скорости не прибегая к его решению. Механическая часть, представленная в виде жесткого звена, как отмечалось, отражает движение системы в среднем и не дает точного представления о характере движения упруго связанных масс. С целью выяснения этого влияния рассмотрим реакцию на скачок момента от 0 до M в двухмассовой системе при нулевых нагрузках M_c1 и M_c2 и нулевых начальных условиях.

Найдем вначале реакцию координаты w₂ , используя ранее полученную передаточную функцию (6.5). Операторное изображение интересующей нас величины при M(p)= M/p равно

w₂(p)= ,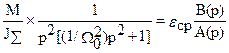

где e _ср - среднее значения ускорения второй массы, B(p)=1 и

A(p)= p²[(1/W₀²)p²+1]-

полином с корнями p_1,2 =0 и p_3,4=±jW₀

Решение найдем по формуле разложения в виде суммы двух составляющих

w₂(t) = w^‘(t) +w^“(t),

первая из которых обусловлена парой нулевых корней, а вторая- парой комплексно-сопряженных корней.

Пользуясь модификацией формулы разложения для случая n кратных корней полинома знаменателя

x(t)=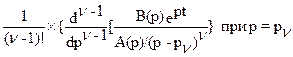

получим

w^‘(t) =

или

w^‘(t) =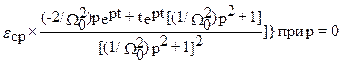

После подстановки p=0, получим

w^‘(t)= e _ср t.

Из курса математики известно, что пара комплексно сопряженных корней p_i,i+1 определяет во временной области составляющую решения вида

x(t)= 2Re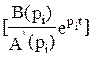

В нашем случае

A’(p)=dA(p)/dp= -2jW ₀

и потому

w^“(t)= e _ср ´2Re = -(e _ср/W₀) Sin W₀t

Таким образом получили окончательное решение

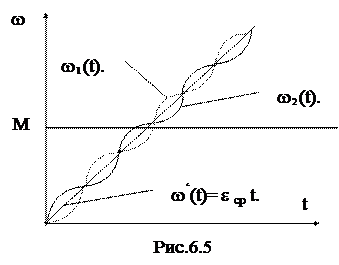
w₂(t) = w^‘(t) +w^“(t) = e _ср t -(e _ср/W₀) Sin W₀t

График зависимости w₂(t) представлен на рис.6.5.. Видно, что скорость w₂ (t) в среднем меняется по линейному закону с ускорением e_ср=M/J_S и содержит незатухающую гармоническую составляющую с амплитудой e _ср/W₀ и частотой W₀.

Определим теперь скорость первой массы, используя выражение для передаточной функции (6.4), которое можно представить в виде суммы

W_w1M(p)= W_w2M(p)+ ,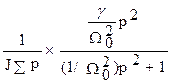

первое слагаемое которой является передаточной функцией W_w2M(p).

Следовательно, решение w₁(t) будет содержать три составляющие, две из которых w^‘(t) и w^“(t) нами уже найдены, а третье можно определить из выражения

w^’”(t) =L^-1 { 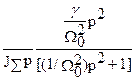´ M/p }

или

w^‘’’(t) =L^-1 { }=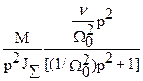

=(e_ср g/W₀²) L^-1 {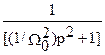

Принимая В(P)=1 и A’(p)= p(2/W₀²) и при p=jW₀ A’(jW₀)= 2j/W₀, получим

w^‘’’(t) =(e_ср g/W₀²) 2Re 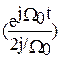= e_ср g/W₀ Sin W₀t

Эта составляющая отмечена штриховой линией на уже рассмот-ренном рисунке. Она находится в противофазе с колебаниями w^’’(t) и потому колебания скорости w₁(t) меньше, чем w₂(t). При прочих равных условиях колебания скорости w₁(t) тем меньше, чем меньше J₂, а увеличение W₀ при тех же ускорениях снижает амплитуды колебаний как первой, так и второй массы. Эти выводы полностью согласуются с результатами частотного анализа. Под действием сил внутреннего вязкого трения эти колебания в действительности являются затухающими во времени, однако время затухания достаточно велико.

Лінійні неоднорідні диференціальні рівняння. Структура загального розв’язку. Метод варіації довільних сталих. Принцип накладання. Лінійні однорідні диференціальні рівняння другого та n-го (n>2) порядку із сталими коефіцієнтами.

Лінійним неоднорідним рівнянням n-го порядку називається рівняння

(6.1)

де функції неперервні на загальний розв’язок рівняння (6.1) має вигляд

(6.2)

Тут – загальний розв’язок лінійного однорідного рівняння яке відповідає рівнянню (6.1), а – який-небудь частинний розв’язок неоднорідного рівняння (6.1).

Якщо відома фундаментальна система розв’язків лінійного однорідного рівняння то загальний розв’язок неоднорідного рівняння (6.1) завжди можна знайти методом варіації довільних сталих (методом Лагранжа). Суть цього методу полягає в тому, що загальний розв’язок неоднорідного рівняння (6.1) шукаємо у вигляді

(6.3)

де функції визначаються із системи

(6.4)

………………………………

Відносно система (6.4) є лінійно неоднорідною алгебраїчною системою. Причому головний визначник цієї системи

(6.5)

Тому система має єдиний розв’язок:

(6.6)

звідки

(6.7)

де – довільні сталі. Врахувавши рівності (6.3) і (6.7), загальний розв’язок рівняння (6.1) запишемо у вигляді

(6.8)

Приклад 1.

Застосовуючи метод Лагранжа, знайти загальний розв’язок рівняння

(6.9)

Розв’язання.

Знайдемо фундаментальну систему розв’язків відповідного однорідного рівняння

(6.10)

Розв’язки рівняння (6.10) шукатимемо у вигляді многочлена Підставивши цей вираз у (6.10) і вписавши лише члени, які містять старший степінь , дістанемо

Прирівнявши до нуля коефіцієнт при , матимемо

звідки

Отже, якщо рівняння (6.10) має розв’язок у вигляді многочлена, то степінь цього многочлена може дорівнювати лише 1, 2 або 3. Безпосередньою перевіркою впевнюємося, що функції утворюють фундаментальну систему розв’язків рівняння (6.10).

Згідно з методом Лагранжа, загальний розв’язок рівняння (6.10) шукаємо у вигляді де функції визначаються із системи

(6.11)

Розв’язавши систему (6.11), дістанемо

звідки

де – довільні сталі.

Отже, загальний розв’язок рівняння (6.9) має вигляд

Принцип накладання (суперпозиції) розв’язків полягає в тому, що коли є розв’язком лінійного неоднорідного рівняння

(6.12)

то функція є розв’язком лінійного неоднорідного рівняння

(6.13)

де Якщо , а є розв’язком неоднорідного рівняння

(6.14)

причому ряд збігається і допускає n -кратне почленне диференціювання, то функція є розв’язком лінійного неоднорідного рівняння

(6.15)

Якщо лінійне неоднорідне рівняння

(6.16)

коефіцієнти якого і функції та – дійсні, має комплексний розв’язок то функції є відповідно розв’язками рівнянь

Приклад 2.

Знайти розв’язок лінійного неоднорідного рівняння

, (6.17)

де – неперервна на функція, який задовольняє нульові початкові умови

. (6.18)

Розв’язання.

Знайдемо фундаментальну систему розв’язків однорідного рівняння

(6.19)

Знизивши порядок рівняння за допомогою заміни де – нова невідома функція, дістанемо рівняння , загальний розв’язок якого – довільна стала. Тоді Звідси

де – довільні сталі. Отже, функції утворюють фундаментальну систему розв’язків рівняння (6.19).

Згідно з методом Лагранжа, загальний розв’язок рівняння (6.17) шукаємо у вигляді

(6.20)

де функції визначаються із системи рівнянь

(6.21)

З (6.21) знаходимо:

,

звідки

(6.22)

,

де – довільні сталі, Підставивши (6.22) у (6.20), дістанемо загальний розв’язок рівняння (6.17):

(6.23)

Із загального розв’язку (6.23) виділимо шуканий частинний розв’язок. Послідовно знаходимо

Початкові умови (6.18) дають систему для визначення

Звідси Отже, шуканий частинний розв’язок

Лінійним однорідним диференціальним рівнянням n-го порядку зі сталими коефіцієнтами називається рівняння виду

, (6.24)

де . Многочлен степеня n виду

(6.25)

називається характеристичним многочленом лінійного диференціального оператора зі сталими коефіцієнтами . Рівняння

(6.26)

називається характеристичним рівнянням оператора .

Розглянемо деякі випадки, які можуть виникнути після розв’язання рівняння (6.26).

1) Якщо – корені рівняння (6.26), причому вони всі є дійсними числами і різні між собою (тобто не існує однакових коренів). Тоді функції

утворюють фундаментальну систему розв’язків рівняння (6.24). Загальний розв’язок рівняння (6.24) матиме вигляд

,

де – деякі дійсні сталі.

2) Якщо – корені рівняння (6.26) з деякою кратністю відповідно , ,причому вони всі є дійсними числами. Тоді функції

,

,

… … … … … … …,

.

утворюють фундаментальну систему розв’язків рівняння (6.24). Загальний розв’язок рівняння (6.24) матиме вигляд лінійної комбінації вказаних функцій і n довільних дійсних сталих.

3) Якщо в рівнянні (6.24) коефіцієнти – дійсні числа, а характеристичне рівняння (6.26) має дійсні корені: – кратності , – кратності , – кратності , а також комплексні корені, які входять комплексно-спряженими парами з однаковою кратністю: – кратності, – кратності, …, – кратності , то фундаментальну систему розв’язків рівняння (6.24) можна вибрати в дійсній формі

Отже, лінійні однорідні рівняння зі сталими коефіцієнтами завжди можна проінтегрувати в елементарних функціях, причому інтегрування зводиться до алгебраїчних операцій.

Приклад 1. Знайти загальні розв’язки рівнянь:

а) б)

Розв’язання.

а) Знаходимо корені характеристичного рівняння Маємо звідки Фундаментальну систему розв’яків утворюють функції , , .

б) Знаходимо корені характеристичного рівняння Маємо звідки Фундаментальну систему розв’язків утворюють функції , , .

Отже,

а)

б)

– довільні сталі.

Приклад 2. Знайти загальний розв’язок рівняння

Розв’язання.

Знаходимо корені характеристичного рівняння

Маємо:

Звідси

Отже,

де – довільні сталі.

Контрольні запитання

1. Яке рівняння називають лінійним неоднорідним диференціальним рівнянням?

2. Яка структура розв’язку лінійним неоднорідним диференціальним рівнянням?

3. Поясніть суть методу Лагранжа розв’язування таких рівнянь.

4. У чому полягає принцип суперпозиції розв’язків, як його застосовувати?

5. Яке рівняння називається лінійним однорідним диференціальним рівнянням?

6. Що таке характеристичний многочлен?

7. Яка загальна структура лінійного однорідного диференціального рівняння зі сталими коефіцієнтами якщо корені характеристичного многочлена дійсні? комплексні?

Дата добавления: 2014-01-14