Формулы Ньютона - Котеса

Лекция 7.

Продолжение контрольной работы №2.

Задача №1.

Имеются следующие данные о реализации молочной продукции в магазинах города по месяцам с 1987 — 1990 г.г. (тыс.т.):

Месяц
январь	5,3	8,3	10,4	5,3
февраль	5,0	7,6	10,2	5,2
март	8,8	11,0	11,8	8,0
апрель	9,8	11,5	14,1	8,2
май	15,4	16,1	17,8	9,8
июнь	18,3	24,8	27,6	14,9
июль	17,1	23,8	25,0	11,8
август	15,4	19,4	19,8	10,3
сентябрь	12,9	15,7	17,4	8,0
октябрь	9,5	11,8	12,7	6,5
ноябрь	9,0	10,2	11,0	5,4
декабрь	7,5	10,1	8,6	5,6

Для изучения общей тенденции реализации данной продукции:

1) произведите преобразование исходных данных путём укрупнения периодов времени: а) в квартальные уровни, б) в годовые уровни;

2) нанесите на линейный график полученные квартальные уровни;

3) произведите сглаживание квартальных уровней с применением пятизвенной скользящей средней;

4) нанесите полученные при сглаживании данные на график с квартальными уровнями;

5) сделайте выводы о характере общей тенденции изучаемого явления.

Задача №2.

Имеются следующие данные о розничном товарообороте за 1984 — 1990 г.г. (тыс. руб.):

483,5	500,7	546,1	570,2	580,7	590,1	611,2

Для изучения общей тенденции развития розничного товарооборота:

1) изобразите ряд динамики в виде линейного графика;

2) произведите аналитическое выравнивание уровней ряда по прямой и выразите общую тенденцию роста соответствующим математическим уравнением;

3) определите выровненные (теоретические) уровни ряда динамики и нанесите их на график с исходными (эмпирическими) данными;

4) сделайте выводы.

Задача №3.

Имеются следующие данные по городу о числе родившихся детей по месяцам 1986 — 1988 гг. (чел.):

Месяц
январь
февраль
март
апрель
май
июнь
июль
август
сентябрь
октябрь
ноябрь
декабрь

Для анализа внутригодовой динамики:

1) определите индексы сезонности, считая, что в ряду динамики отсутствует тенденция развития;

2) представьте в виде линейного графика сезонную волну;

3) сделайте соответствующие выводы.

Здесь мы рассмотрим интерполяционные квадратурные формулы, в которых весовая функция , а узлы расположены равномерно на промежутке [a,b], причем концы промежутка обязательно являются узлами, т.е. 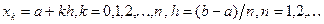. Таким образом, наименьшее число узлов — 2, т.е. точки a и b.

Рассмотрим некоторые наиболее часто встречающиеся формулы.

1. Формула трапеций. В качестве узлов берем точки 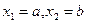. Квадратурная формула будет иметь вид:

(4.1)

Найдем коэффициенты A₁ и A₂:

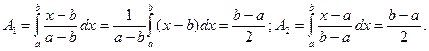
Значит

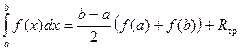(4.2)

Геометрический смысл формулы трапеций: Мы заменяем площадь под кривой

площадью трапеции, как изображено на рисунке.

Отсюда и название — формула трапеций.

Теперь рассмотрим вопрос об остаточном члене

формулы трапеций. Пусть функция f (x) имеет непрерывную 2-ю производную всюду на [a,b]. Тогда

(4.3)

Запишем остаточный член интерполирования функции f (x) по узлам a и b:

и x зависит от х.

Проинтегрируем левую и правую часть этого равенства по х:

.

Функция , стоящая под знаком интеграла, не меняет знак на [a,b], а непрерывна на [a,b] по предположению. Значит можно применить обобщенную теорему о среднем. Тогда .

Таким образом получаем

(4.4)

Дата добавления: 2014-01-14