Построение эмпирической кривой обеспеченности стока

Для построения эмпирической кривой обеспеченности необходимо величины годового стока расположить в убывающем порядке от наибольшего значения к наименьшему. Такой ряд дает общее представление о колебании значений годового стока за период наблюдений.

Обеспеченность каждого члена ряда, расположенного в убывающем порядке, выраженная в процентах (или в долях единицы), может быть вычислена по формуле

(32)

где Р - обеспеченность данного расхода в процентах, m -порядковый номер данного расхода в ряду, n- общее число членов ряда.

В последнее время для построения эмпирических кривых обеспеченности годового стока получил большее распространение, как более обоснованная формула

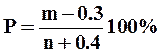
(33)

Эмпирическая кривая обеспеченности может быть построена в прямоугольных координатах или специальной сетке так называемой клетчатке вероятностей. По оси ординат откладываются значения годовых расходов (или модульных коэффициентов), а по оси абсцисс - значения обеспеченности (в процентах) этих расходов, вычисленные по формулам (32) или (33). Нанесенные точки соединяются плавной кривой.

Как видно из формул (32) и (33), обеспеченность крайних точек является наименее достоверной и наименее устойчивой из всех точек. И зависит от длительности ряда наблюденй. Предпочтительнее строить кривую обеспеченности на клетчатке вероятностей. При этом кривые распрямляются.

Эмпирическая кривая обеспеченности позволяет определять расчетные значения гидрологической характеристики Q_р, заданной вероятности превышения Р.

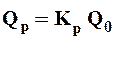
(34)

где К_р - ордината кривой обеспеченности, соответствующая заданному значению Р%; Q₀ - среднее арифметическое значение (норма) гидрологической характеристики.

Зная эмпирическую обеспеченность гидрологической характеристики, можно подсчитать вероятность повторяемости в годах, т.е. число лет N, в течение которых данное значение характеристики встречается в среднем один раз. Обеспеченность Р и повторяемость N связаны между собой следующим образом.

при Р< 50% (35)

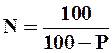при Р> 50% (36)

Полученная на основе ограниченного числа фактических наблюдений эмпирическая кривая обеспеченности недостаточно точно и полно отражает закономерности изменения гидрологической характеристики. Особенно слабо освещены данными наблюдений концевые участки кривой, относящиеся к области больших и малых значений исследуемой характеристики стока, представляющие как раз наибольший интерес при решении ряда инженерных задач (например, при расчетах максимального и минимального стоков). Поэтому в гидрологии широко применяют аналитические (то есть, описываемые определенными уравнениями) функции распределения, которые наилучшим образом отвечают не только случайным выборкам, но и всему процессу колебаний характеристик стока в целом (генеральной совокупности).

2. Построение аналитической кривой обеспеченности стока. Аналитическая кривая обеспеченности при известных параметрах Q₀, C_v и C_s строят с помощью таблиц, приведенные в работе "Практикум по гидрологии, гидрометрии и регулированию стока. М.; Агропромиздат,1998"(Приложение 2, с.215). В данной работе представлены результаты интегрирования соответствующих кривых распределения. Ординаты кривой обеспеченности, представленные в этих таблицах даны в виде модульных коэффициентов для значений обеспеченности P% от 0,001 до 99,9 % при различных коэффициентах вариации C_v - от 0,1 до 1,0.

Ординаты аналитических кривых обеспеченности определяют следующим образом:

1. Выбирают таблицу соответствующую определенному соотношению C_s/C_v.

2. По выбранной таблице для заданного коэффициента вариации C_v выписывают значения K_P при различных значениях P%. Если заданный коэффициент вариации C_v не совпадает с табличным, то проводят интерполирование.

3. Определяют абсолютные ординаты кривой обеспеченности

Q_P=K_PQ₀

По вычисленным ординатам строят график аналитической кривой обеспеченности трехпараметрического гамма распределения.

Дата добавления: 2014-01-14