Тест 3

Теперь найдём точку пересечения прямой линии PQ с плоскостями EAB, EBC и EAC. Вычислим значения параметров l для точки пересечения прямой линии PQ с плоскостью EAB по уравнению (8.5) и m для точки пересечения прямой AB с плоскостью EPQ по уравнению (8.8). (В обоих случаях прямая линия может оказаться параллельной плоскости, поэтому параметрам l и m будут присвоены очень большие числа.) Уравнение (8.4) описывает плоскость EAB. Если левая часть этого уравнения при подстановке координат точек P и C принимает разные знаки, то это означает, что точки P и C лежат по разные стороны от прямой AB. Тогда можно сказать, что точка P лежит за прямой AB. Если точка лежит за одной из сторон треугольника, то она расположена вне этого треугольника.

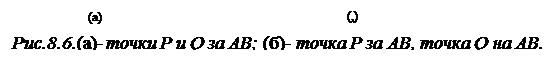Запомним эту информацию в логической переменной Poutside («точка P вне»). Аналогично для точки Q введена переменная Qoutside («точка Q вне»).Эти переменные будут проверяться в тестах 4 и 6. Если точки P и Q лежат за одной и той же стороной треугольника или одна точка находится за стороной, а другая - точно на этой стороне, то будем говорить, что отрезок PQ лежит вне этого треугольника. Тогда отрезок PQ - видимый. Обе ситуации показаны на рисунке 8.6. Важный специальный случай возникает при небольшой модификации рис. 8.6(б), когда точка Q совпадает с точкой A. Заметим, что в отличие от рисунка 8.5(б) бесконечная прямая линия PQ на рисунке 8.6(б) может пересекать отрезок BC между точками B и C так, что тест 3 будет выполнен в том случае, когда тест 2 оказался невыполненным.

Большая часть работы должна быть выполнена трижды, а именно: для каждой из плоскостей EAB, EBC и ECA, следовательно, будем иметь три пары значений (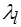, 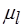) (l = 1,2,3). Затем найдём минимальное и максимальное из значений 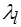, удовлетворяющие условиям

0 <= l <= 1 и 0 <= m <= 1

и эти значения обозначим MIN и MAX, соответственно. Они являются побочным продуктом этого теста и определяются только тогда, когда отрезок PQ пересекает треугольник, то есть если тесты 3 и 4 (см. ниже) не выполнены.

Тест 4 (рис. 8.7).

Если и точка P, и точка Q находятся внутри пирамиды, а предыдущий тест не удовлетворён, то отрезок PQ лежит позади треугольника и, следовательно, невидим.

При выполнении этого теста также может встретиться весьма хитрая ситуация. Предположим, например, что отрезок PQ лежит на пирамиде позади отрезка AB. Поскольку отрезок PQ не находится ни снаружи, ни внутри пирамиды, то кажется сомнительным, можем ли мы сказать, что треугольник закрывает отрезок PQ. Однако отрезок AB может быть не ребром, а диагональю грани. Тогда эта грань определённо закрывает отрезок и он не должен вычерчиваться. С другой стороны, если бы отрезок AB был ребром объекта, то и тогда отрезок PQ вычерчивать было бы не нужно, поскольку изображение отрезка PQ совпадало бы с ребром AB, а чертить совпадающие отрезки линий нет никакого смысла.

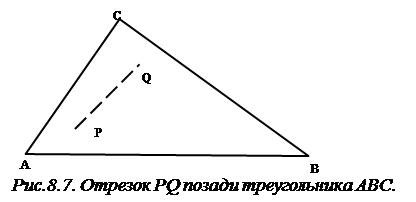Тест 5 (рис 8.8).

Если точка I, в которой прямая линия PQ пересекает пирамиду, лежит впереди треугольника, то прямая PQ видима. Этот тест основан на том факте, что объект является сплошным телом, поэтому прямая PQ не может проходить через внутренние точки треугольника. Для нахождения такой точки I используем значения MIN и MAX параметра l, вычисленные при выполнении теста 3. Затем можно просто проверить, не будет ли скалярное произведение векторов EI и n =[ abc ] меньше, чем h.

Дата добавления: 2014-01-14