Лекція 8

Інтегрування диференціальних рівнянь за допомогою степеневих рядів. Системи диференціальних рівнянь. Нормальна система. Геометричний зміст розв’язків. Задача Коші для нормальної системи рівнянь. Теорема існування та єдиності розв’язку задачі Коші. Загальний та частинний розв’язки. Розв’язання нормальної системи рівнянь методом виключення.

Розв’язки лінійного диференціального рівняння вище першого порядку зі змінними коефіцієнтами не завжди виражаються через елементарні функції, інтегрування такого рівняння досить рідко зводиться до квадратур. На практиці широко використовується метод зображення шуканого розв’язку у вигляді степеневого ряду.

Розглянемо рівняння другого порядку

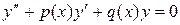. (8.1)

Припустимо, що коефіцієнти 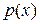і рівняння (8.1) є аналітичними функціями на інтервалі 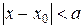, тобто

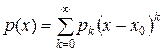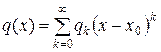, , (8.2)

.

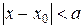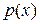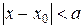Теорема. Якщо функції і – аналітичні при , то будь-який розв’язок 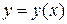рівняння (8.1) є аналітичною функцією на інтервалі 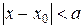, тобто

,

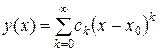причому степеневий ряд збігається на інтервалі .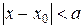

Сформульована теорема дає змогу побудувати розв’язки рівняння (8.1) у вигляді степеневих рядів. Поклавши для спрощення викладок , розв’язок рівняння (8.1) шукатимемо у вигляді степеневого ряду за степенями :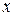

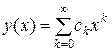(8.3)

з невизначеними коефіцієнтами.

Підставивши (8.3) в рівняння (8.1), отримаємо

.

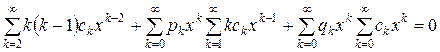Прирівнюючи до нуля коефіцієнти при степенях 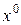, , 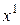…, дістанемо рекурентну систему рівнянь для визначення невідомих коефіцієнтів 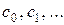. Коефіцієнти і 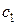можна задавати довільно, але хоча б один з них повинен бути відмінним від нуля, інакше отримаємо розв’язок 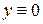. Зафіксувавши і 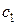, шукаємо розв’язок рівняння (8.1), який задовольняю початковим умовам 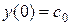, 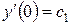. З першого рівняння знаходимо 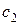, з другого – 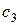і т.д.

Приклад 1. Розв’язати рівняння .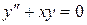

Розв’язування. Коефіцієнти 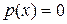та 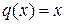є аналітичними функціями при всіх .

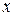Розв’язки шукаємо у вигляді ряду

.

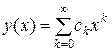Підставляємо цей ряд у дане рівняння:

.

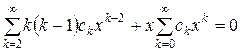Прирівнявши до нуля коефіцієнти при степенях 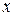у лівій частині, отримаємо рекурентну систему рівнянь для визначення :

, ,

, …., , …

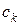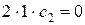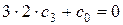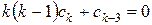звідки

, ,

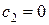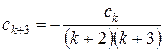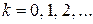
Поклавши 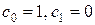. Тоді відмінними від нуля будуть лише коефіцієнти .

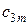Маємо

,

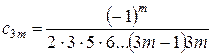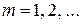
Побудовано розв’язок рівняння

.

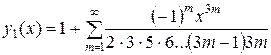Другий розв’язок, лінійно незалежний з 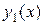, отримаємо, поклавши 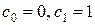. Тоді відмінними від нуля будуть лише коефіцієнти :

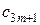Маємо

,

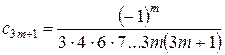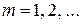
Тому

.

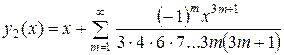І загальний розв’язок даного рівняння має вигляд

,

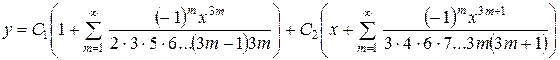де 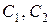– довільні сталі. Отже, будь-який розв’язок даного рівняння є аналітичною функцією при всіх .

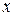Сукупність співвідношень виду

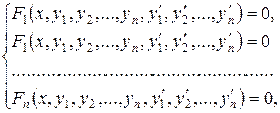(8.4)

де 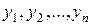– шукані функції від незалежної змінної 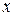, називається системою звичайних диференціальних рівнянь першого порядку. Всяка сукупність 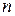функцій

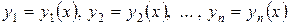(8.5)

визначений і неперервно диференційований на інтервалі , називається розв’язком системи (8.4) в цьому інтервалі, якщо вона перетворює всі рівняння системи (8.4) в рівності, справедливі при всіх значеннях 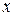з інтервалу . Процес знаходження розв’язків системи (8.4) називається інтегруванням цієї системи. Графік розв’язків (8.5) називається інтегральною кривою системи (8.4).

Приклад 2. Розглянемо систему

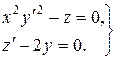(8.6)

Розв’язування.

Ця система має розв’язок

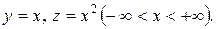(8.7)

Дійсно, підставляючи (8.7) в (8.6), дістаємо рівності

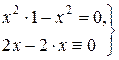
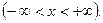
Система диференціальних рівнянь

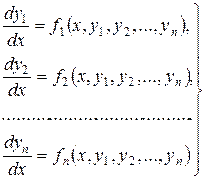(8.8)
розв’язана відносно похідних від шуканих функцій, називається системою диференціальних рівнянь в нормальній формі або нормальною системою.

Якщо за допомогою деяких перетворень з даної нормальної системи вдається отримати інтегровне рівняння, то така система називається інтегрованою комбінацією.

Приклад 3. Розв’язати систему

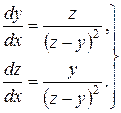(8.9)

Розв’язування. Це нормальна система. Поділивши перше рівняння на друге, дістанемо інтегровну комбінацію

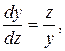
звідки

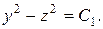(8.10)

Віднявши почленно друге рівняння системи (8.9) з першого, дістанемо ще одну інтегровну комбінацію

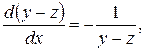
звідки

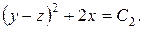(8.11)

Сукупність співвідношень виду (8.10) і (8.11) в загальній теорії диференціальних рівнянь називається загальним інтегралом системи.

Якщо праві частини нормальної системи лінійно залежать від шуканих функцій 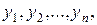тобто ця система має вигляд

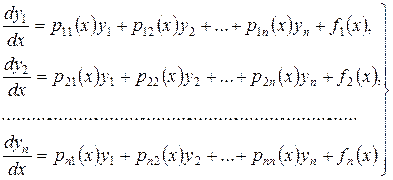(8.12)

то вона називається лінійною системою. Із лінійних систем найбільш важливими, як в теорії, так і в застосуваннях, є системи з постійними коефіцієнтами.

Початкова задача або задача Коші для нормальної системи (8.8), ставиться так: знайти розв’язок (2), що задовольняє початкові умови (умови Коші)

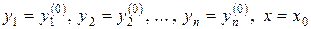(8.13)

де 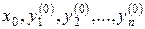– задані числа. Геометрично це означає, що слід знайти інтегральну криву, що проходить через дану точку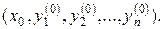

Розглянемо нормальну систему виду

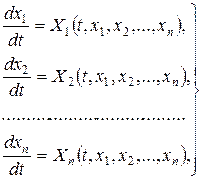(8.14)

де 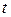– час, а 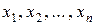– координати точки 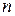-вимірного простору. Цей простір будемо називати фазовим простором. У випадку 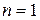фазовий простір є вісь 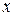; при 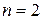– площина 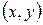– фазова площина.

Будь-який розв’язок

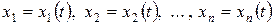(8.15)

визначає інтегральну криву системи (8.14) та є законом руху точки в фазовому просторі. Тому розв’язок (8.15) називають просто рухом, який визначає система диференціальних рівнянь (8.14), а шлях, що описує точка в фазовому просторі,– траєкторією цього руху.

Ліві частини системи (8.14) суть складові (по осях координат) швидкості руху точки. Тому система (8.14) задає так зване поле швидкостей руху так, що точка може проходити в момент часу 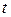через положення 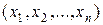тільки з заданою швидкістю. Потрібно знайти самі рухи і вивчити їх властивості. Якщо швидкість, з якою точка проходить через положення 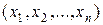, не залежить явно від моменту часу проходження, тобто система (8.14) має вигляд

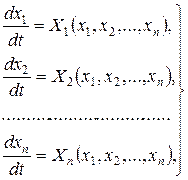(8.16)

то вона називається стаціонарною або автономною системою.

Якщо система (8.14) така, що в деякій точці 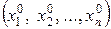її праві частини рівні нулю при всіх розглянутих значеннях часу 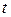, тобто

то система має розв’язок

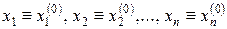(8.17)

Рух (8.17) називається станом спокою. Траєкторією цього руху є точка – точка спокою.

Задача Коші, або початкова задача для системи (8.14), полягає в знаходженні руху (8.15), що задовольняє початковим умовам

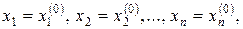при (8.18)

де 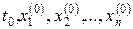– задані числа (початкові дані), тобто шукається такий рух, при якому точка, що рухається, знаходиться в заданій точці фазового простору в заданий момент часу 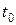. При цьому точка називається початковою точкою руху (8.15).

Зазначимо, що якщо початкова точка руху (8.15) є точкою спокою , то одним із розв’язків задачі Коші є стан спокою (8.17).

Приклад 4. Розглянемо систему

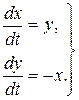(8.19)

Знайдемо рухи, що визначається цією системою, і вивчимо їх властивості. Зазначимо, що система (8.19) автономна. Початок координат 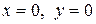є точкою спокою, так як праві частини системи (8.19) перетворюються в нуль при всіх значеннях часу 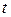. Цій точці відповідає рух

стан спокою. (8.20)

Знайдемо всі інші рухи і вияснимо, як вони ведуть себе по відношенню до стану спокою (8.20). Проведемо спочатку попереднє дослідження характеру руху, що визначається системою (8.19). Для цього вивчимо поле швидкостей.

В точках осі 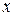маємо

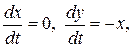
тобто складова швидкості по осі 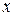дорівнює нулю, а складова по осі 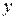залежить від .

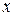Проінтегруємо тепер систему (8.19). Бажаючи виключити одну невідому функцію, наприклад 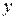, знайдемо похідні по 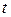від обох частин першого рівняння системи і замінимо 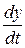її значенням з другого рівняння. Отримаємо

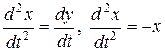
або

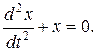(8.21)

Рівняння (8.21) має загальний розв’язок

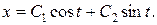
Так як 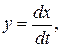то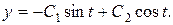

Таким чином всі розв’язки системи (8.19) даються формулою

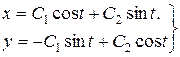(8.22)

З цієї формули видно, що всякий розв’язок системи (8.19) 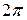-періодичний і обмежений при .

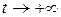Виключивши з рівнянь рухів (8.22) час 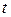, знайдемо траєкторію рухів:

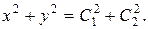
Це кола з центром в початку координат (в точці спокою системи (8.19)).

Знайдемо рух, що задовольняє початковим умовам

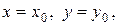при 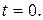(8.23)

Замінюючи в (8.22) змінн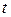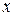і , і 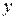числами 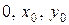, маємо

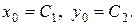
Підставляючи ці значення будь-яких сталих в (8.22), отримаємо

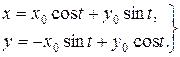(8.24)

Інших розв’язків немає, так як (8.22) містить всі розв’язки системи (8.19).

Якщо 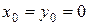, то рух (8.24) перейде в стан спокою (8.20).

Якщо початкові дані не рівні одночасно нулю, але достатньо малі, то відповідні їм рухи (8.24) будуть як завгодно близькі до стану спокою при всіх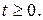

Аналогічно, як і для нормального диференціального рівняння можна сформулювати теорему існування і єдиності розв’язку для нормальної системи (8.8).

Теорема Пікара. Якщо праві частини системи (8.8) неперервні в деякій області початкової точки 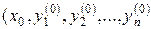) і мають неперервні в цій області часткові похідні по 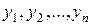, то така система має єдиний розв’язок (8.5) в деякій області точки 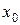, що задовольняє початковим умовам (8.13).

Умови теореми Пікара виконуються, якщо праві частини нормальної системи поліноми відносно 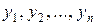, коефіцієнти яких неперервні в області початкового значення 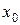. При цьому початкові значення 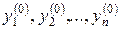можна брати довільно.

Теорема Пікара для лінійної системи (8.12) має такі ж дві особливості, що і в випадку лінійного рівняння першого порядку:

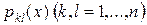1) початкові значення шуканих функцій можна задавати довільно, а початкове значення незалежної змінної можна брати будь-яким з інтервалу , в якому коефіцієнти і функції 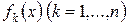неперервні;

2) розв’язок задачі Коші визначений і неперервно диференційовний на всьому інтервалі .

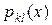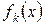Якщо всі і неперервні при всіх значеннях 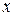, то всі початкові дані можна вибирати абсолютно вільно, і розв’язок існує при всіх .

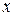Задачу Коші для нормальної системи (8.8) не завжди вдається розв’язати в точному вигляді, тому виникає необхідність побудови наближених методів знаходження розв’язків задачі Коші.

Розглянемо нормальну систему (8.8)

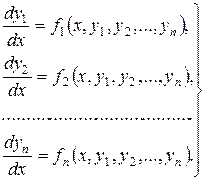
Нехай 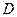є область в просторі 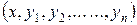, через кожну точку якої проходить одна і тільки одна інтегральна крива системи (8.8). Для цього достатньо припустити, що в кожній точці області 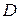функції 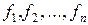неперервні відносно всіх своїх аргументів і мають неперервні часткові похідні по .

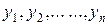Сукупність 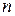функцій

(8.25)

визначених в деякій області зміни змінних 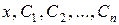і неперервно диференційованих відносно 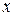, називається загальним розв’язком системи (8.8) в області 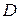, якщо:

1) система (8.25) розв’язується в області 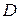відносно довільних сталих :

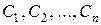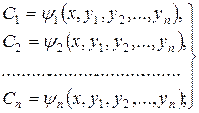(8.26)

2) сукупність функцій (8.25) є розв’язком системи (8.8) при всіх значеннях довільних сталих 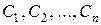, що визначаються формулами (8.26), коли точка 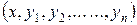пробігає область .

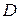Значення загального розв’язку (8.25) дає можливість розв’язати задачу Коші з будь - якими початковими даними 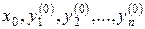з області 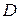за рахунок вибору відповідних значень довільних сталих 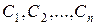. Для цього достатньо замінити в (8.25) величини 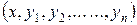початковими даними :

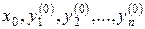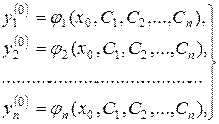(8.27)

розв’язати систему (8.27) відносно :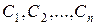

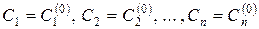
і підставити знайдені значення довільних сталих в (8.25). Отримаємо

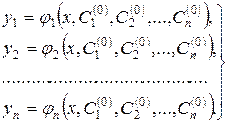
Це і є оптимальний розв’язок. Він єдиний.

Якщо в загальному розв’язку (8.25) роль довільних сталих 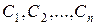відіграють початкові значення 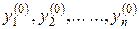шуканих функцій 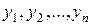при деякому фіксованому значенні 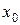незалежної змінної

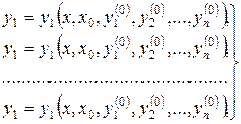
то такий запис загального розв’язку будемо називати загальним розв’язком в формі Коші.

Приклад 5. Розглянемо систему

(8.28)

Це є лінійна система з постійними коефіцієнтами; вона може бути проінтегрована послідовно, так як перше рівняння не містить 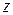. Інтегруючи це рівняння, підставляємо загальний розв’язок в друге рівняння і інтегруючи отримане рівняння, знайдемо 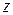. Маємо

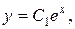
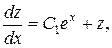
звідки

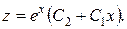
Сукупність функцій

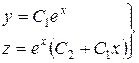(8.29)

є загальним розв’язком системи (8.28) у всьому просторі .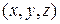

Дійсно, в околі будь-якої точки 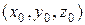виконуються умови теореми Пікара, тому через цю точку проходить одна і тільки одна інтегральна крива ситеми (8.28).

Сукупність функцій (8.28) задовольняє обидві умови, вказані у визначенні загального розв’язку:

1) система (8.29) розв’язується відносно і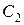у всьому просторі :

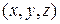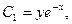
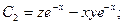
2) функції (8.29) утворюють розв’язок системи (8.28) при всіх значеннях і 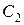. Тому (8.29) є загальним розв’язком системи (8.28) у всьому просторі .

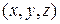Знайдемо розв’язок з початковими даними 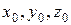. Розв’язуючи систему

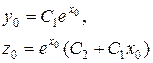
відносно і 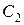, знайдемо

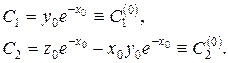
Остаточним розв’язком буде

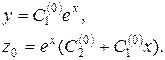
Зокрема, при будемо мати

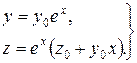(8.30)

Якщо в (8.30) рахувати 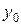і довільними, то отримаємо загальний розв’язок системи (8.28) в формі Коші.

Розв’язок нормальної системи диференціальних рівнянь називається частковим, якщо в кожній його точці мають місце існування і єдиність розв’язку задачі Коші. Будь-який розв’язок, що знаходиться в формулі загального розв’язку є частковим розв’язком. Наприклад (8.30) є частковим розв’язком системи (8.28).

Рівняння 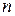-го порядку (8.22)

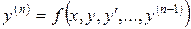
завжди можна звести до нормальної системи 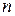рівнянь. З цією метою позначимо шукану функцію 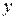через і приймемо 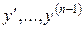за нові невідомі функції, поклавши

(8.31)

складемо систему диференціальних рівнянь для функцій 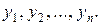Маємо

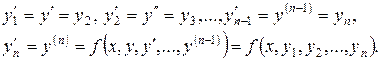
Тому для функцій 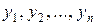отримаємо наступну нормальну систему диференціальних рівнянь:

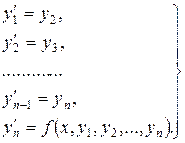(8.32)

Знайшовши розв’язок системи (8.31), знайдемо і розв’язок рівняння (8.22), так як .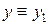

Якщо рівняння 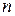-го порядку лінійне, то і відповідна йому нормальна система буде лінійною.

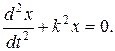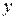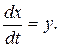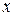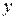Приклад 6. Розглянемо рівняння Зведемо його до нормальної системи двох рівнянь; введемо невідому функцію , поклавши Тоді для і отримаємо нормальну систему:

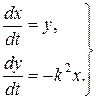
Нехай дана нормальна система 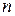рівнянь (8.8)

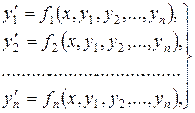
Одним із способів інтегрування цієї системи поряд з методом інтегрованих комбінацій є так званий метод виключення. Він полягає в тому, що з системи (8.8) за допомогою диференціювання одного з рівнянь і заміни 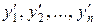їх значеннями, із системи (8.8) намагаються виключити всі шукані функції, крім однієї, для якої отримаємо рівняння 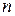-го порядку. Знайшовши загальний розв’язок цього рівняння, знаходимо решту невідомих функцій без подальших квадратур.

На практиці не завжди вдається звести даним способом систему (8.8) до одного рівняння 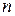-го порядку, але можна довести, що тоді система (8.8) зводиться до групи рівнянь (з однією невідомою функцією кожне), сума порядків яких рівна .

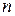Приклад 7. Розв’язати систему

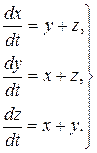(8.33)

Розв’язування. Диференціюючи перше рівняння і користуючись другим і третім, отримуємо

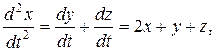
але тому

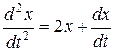
або

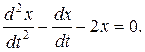(8.34)

Отримали одне рівняння другого порядку. Згідно сказаного вище, потрібно отримати ще одне рівняння першого порядку з однією невідомою функцією: 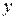або 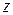. Виключимо 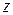з перших двох рівнянь системи (8.33). Віднімаючи почленно перше рівняння з другого, маємо

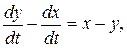
звідки

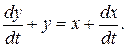(8.35)

Це і є шуканим рівнянням першого порядку з однією невідомою функцією 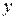(права частина рівняння (8.35) є відома функція від 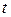, так як 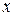визначається з рівняння (8.34)). Проінтегрувавши послідовно рівняння (8.34), (8.35), знайдемо 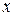і 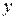, після чого знайдемо :

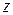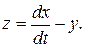(8.36)

З рівняння (8.34) знайдемо

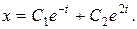(8.37)

Підставляючи в (8.35), маємо

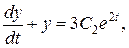
звідки

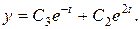(8.38)

Нарешті, з (8.36) знайдемо :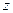

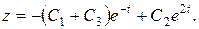(8.39)

Формули (8.37), (8.38) і (8.39) утворюють загальний розв’язок системи (8.33) в області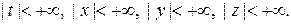

Контрольні запитання

1. Що називається системою звичайних диференціальних рівнянь? її інтегруванням? інтегральною кривою?

2. Яка система дифрівнянь називається нормальною?

3. Що називається загальним інтегралом нормальної системи?

3. Сформулюйте задачу Коші для нормальної системи диференціальних рівнянь.

4. Поясніть механічну суть нормальної системи дифрівнянь.

5. Сформулюйте теорему Пікара, поясніть її суть.

6. Що є загальним, частковим, особливим розв’язком нормальної системи дифрівнянь?

7. Як звести нормальну систему дифрівнянь до одного рівняння і навпаки дифрівняння 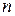-го порядку до нормальної системи?

8. Поясніть суть методу виключення.

Дата добавления: 2014-01-14