Лекція 9

Нормальна система лінійних рівнянь, векторно - матричний запис. Теорема існування та єдності розв’язку задачі Коші. Структура загального розв’язку лінійної однорідної та лінійної неоднорідної системи. Розв’язування нормальної системи лінійних диференціальних рівнянь із сталими коефіцієнтами. Метод Ейлера.

Система диференціальних рівнянь

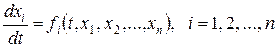, (9.1)

називається системою в нормальній формі або системою, розв’язаною відносно похідних шуканих функцій .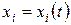

Розв’язком системи рівнянь (9.1) на проміжку 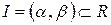називається сукупність неперервно диференційовних на 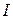функцій 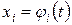, , 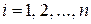таких, що

.

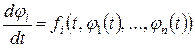
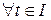Рівність 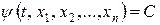, де 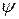– неперервно диференційована в області визначення системи (9.1) функція, С – довільна стала, називається першим інтегралом цієї системи, якщо має місце рівність

.

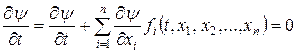Якщо відомо 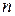незалежних перших інтегралів 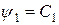, , 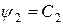…, , 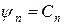то сукупність

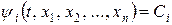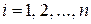, , (9.2)

де 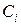– довільні сталі, визначає загальний інтеграл системи (9.1).

Із загального інтеграла, розв’язуючи рівності (9.2) відносно 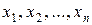, можна знайти практично будь-який розв’язок системи (9.1).

Якщо відомий відмінний від сталої один перший інтеграл 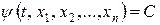, то, розв’язуючи це рівняння відносно однієї із змінних, наприклад, відносно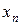

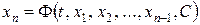(9.3)

і підставляючи вираз (9.3) в перші 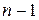рівняння системи (9.1), отримаємо систему рівнянь, в якій число невідомих функцій на одиницю менше, ніж в системі (9.1).

Векторно – матричний запис лінійної однорідної системи диференціальних рівнянь має вигляд

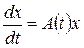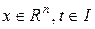, , (9.4)

де 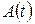– квадратна матриця порядку 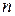, елементи якої 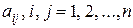, – неперервні на інтервалі 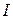функції. Будь-який розв’язок системи (9.4) можна продовжити на весь інтервал .

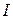Матриця , стовпцями якої є розв’язки, що утворюють фундаментальну систему, називається фундаментальною матрицею.

Якщо 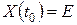, де 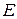– одинична матриця, то фундаментальна матриця називається матрицантом системи (9.4).

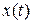Будь – яка система вигляду (9.4) завжди має фундаментальну матрицю . Будь – який розв’язок системи (9.4) можна записати у вигляді

,

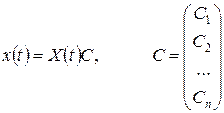де 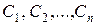– сталі, тобто 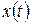є лінійною комбінацією розв’язків фундаментальної системи.

Приклад 1. Розглянемо систему

.

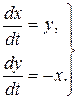Розв’язування.

Загальний розв’язок цієї системи, знайдений методом виключення, має вигляд

.

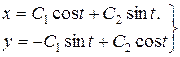Підставивши в отриманий розв’язок спочатку 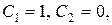а потім 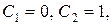отримаємо два часткових розв’язки

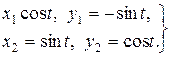(9.5)

Ці часткові розв’язки лінійно залежні в будь-якому інтервалі, так як

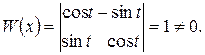
Звідси, часткові розв’язки (9.5) утворюють фундаментальну систему розв’язків (в будь-якому інтервалі зміни ).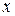

Знання фундаментальної системи розв’язків дає можливість побудувати загальний розв’язок однорідної лінійної системи. А саме: можна довести, що якщо розв’язки утворюють фундаментальну систему розв’язків однорідної лінійної системи в інтервалі 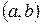, то лінійна комбінація цих розв’язків з будь-якими постійними коефіцієнтами 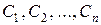, тобто функції

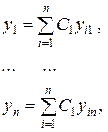
утворюють загальний розв’язок системи в області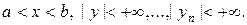

Лінійною неоднорідною системою називається система вигляду

, ,

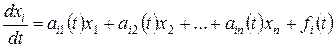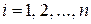або у векторно – матричній формі

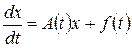, (9.6)

де 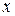– вектор з компонентами 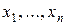; 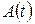– матриця, елементами якої є функції 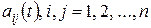; 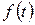– вектор – функція з компонентами .

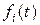Якщо відома фундаментальна матриця лінійної однорідної системи (9.4), то систему (9.6) завжди можна розв’язати за допомогою методу варіації довільних сталих (методу Лагранжа).

Згідно з цим методом, загальний розв’язок рівняння (9.6) шукаємо у вигляді 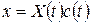. Компоненти 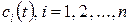, вектора 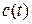визначаються із системи рівнянь

,

яка має єдиний розв’язок відносно .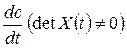

Систему (9.6) можна також розв’язувати за допомогою методів виключення та інтегрованих комбінацій.

Загальний розв’язок лінійної неоднорідної системи (9.6) складається із загального розв’язку лінійної однорідної системи (9.4) і якого – небудь частинного розв’язку неоднорідної системи (9.6).

Системою лінійних диференціальних рівнянь зі сталими коефіцієнтами називають систему вигляду

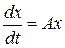, (9.7)

де 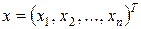– 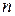-вимірий вектор, 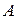– дійсна стала квадратна матриця порядку 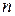. Цю систему можна методом виключення звести до лінійного рівняння зі сталими коефіцієнтами відносно однієї невідомої функції. Проте існують і інші методи розв’язування таких систем.

Розглянемо метод Ейлера розв’язування систем вигляду (9.7). Згідно з цим методом розв’язки системи (9.7) шукають у вигляді

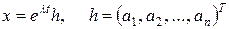. (9.8)

Функція (9.8) є розв’язком системи (9.7) тоді і тільки тоді, коли – власне значення матриці 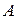, а 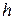– власний вектор цієї матриці, який відповідає числу . Якщо власні значення 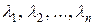матриці 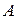попарно різні, а 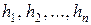– відповідні їм власні вектори, то загальний розв’язок системи (9.7) має вигляд

,

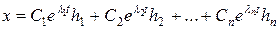де 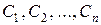– довільні числа.

Якщо власному значенню кратності 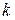відповідає рівно 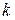лінійно незалежних власних векторів 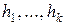, то система (9.7) має 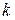лінійно незалежних розв’язків вигляду .

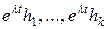Якщо власному значенню кратності 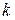відповідає 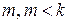, лінійно незалежних власних векторів, то розв’язки, які відповідають , можна шукати у вигляді

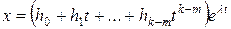, (9.9)

де 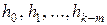– невідомі вектори. Щоб знайти координати невідомих векторів 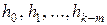, треба підставити вираз (9.9) у систему (9.7). Прирівнявши коефіцієнти подібних членів у лівій і правій частинах системи, отримаємо рівняння для визначення координат невідомих векторів.

Якщо серед власних значень матриці 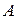є комплексно спряжені пари чисел 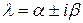, , 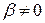то розглянутим способом можна побудувати відповідні їм комплексні розв’язки виду 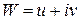. Виділивши дійсну і уявну частини таких розв’язків, отримаємо дійсні розв’язки, які відповідають .

Приклад 2. Розглянемо систему

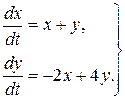(9.10)

Розв’язування.

Шукаємо частковий розв’язок системи (9.10) у вигляді

(9.11)

Складемо характеристичне рівняння

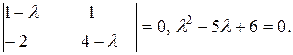
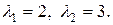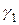Воно має корені Побудуємо частковий розв’язок вигляду (9.11), що відповідає розв’язку . Числа і 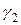потрібно шукати з системи

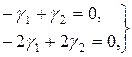
яка зводиться до одного рівняння

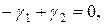
так що одне з чисел 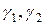можна вибрати довільно. Але при цьому потрібно піклуватись про те, щоб числа 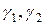не були одночасно рівними нулю. Припустимо, 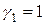, дістанемо 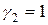; тому характеристичному числу відповідає частковий розв’язок

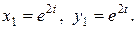(9.12)

Аналогічно знаходимо частковий розв’язок, що відповідає характеристичному числу :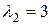

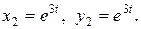(9.13)

Розв’язки (9.12) і (9.13) утворюють фундаментальну систему розв’язків. Загальним розв’язком системи (9.10) буде

.

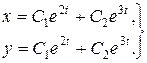Приклад 3. Розглянемо знову систему

.

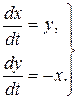Розв’язування.

Характеристичне рівняння вигляду

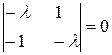або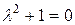

має корені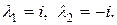

Побудуємо комплексний розв’язок, що відповідає кореню 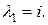Він має вигляд

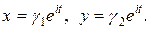
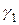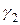Числа і визначаються з рівняння

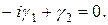
(Система 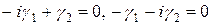зводиться до одного рівняння).

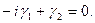
Припустивши 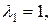знаходимо 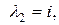так що

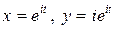
або

Відділяючи в цьому комплексному розв’язку дійсні і умовні частини, дістанемо два дійсні часткові розв’язки, що утворюють фундаментальну систему розв’язків.

Загальний розв’язок, має вигляд

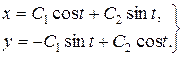
Розглянемо окремі випадки розв’язування системи лінійних диференціальних рівнянь вигляду (9.6).

Якщо в системі (9.6) матриця 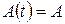– стала, а функції 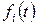мають вигляд

,

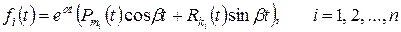де 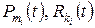– многочлени степенів 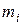та 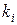відповідно, то частинний розв’язок неоднорідної системи (9.6) може бути знайдений за методом невизначених коефіцієнтів.

За цим методом, частинний розв’язок шукаємо у вигляді

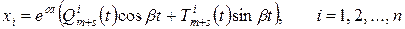(9.14)

де 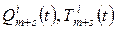– многочлени степеня 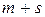з невизначеними коефіцієнтами, 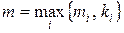, , 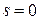якщо контрольне число 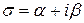не є власним значенням матриці 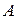; якщо ж 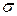є власним значенням матриці 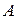, то 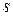можна вибрати таким, що дорівнює кратності цього числа.

Невідомі коефіцієнти 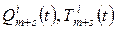знаходять за допомогою підстановки (9.14) в дану систему і прирівнювання коефіцієнтів подібних членів.

Контрольні запитання

1. Який вигляд лінійної системи диференціальних рівнянь в нормальній формі? Чим відрізняється однорідна лінійна система від неоднорідної?

2. Що називається першим інтегралом нормальної системи лінійних диференціальних рівнянь?

3. Як записати лінійну однорідну систему диференціальних рівнянь у векторно – матричній формі?

4. Що таке фундаментальна система розв’язків однорідної лінійної системи 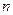рівнянь?

5. Що таке фундаментальна матриця? Матрицант?

6. Як записати загальний розв’язок системи лінійних однорідних диференціальних рівнянь?

7. Яка структура загального розв’язку системи лінійних неоднорідних дифрівнянь?

8. Що називається системою лінійних диференціальних рівнянь зі сталими коефіцієнтами?

9. У чому полягає метод Ейлера побудови фундаментальної системи розв’язків однорідної лінійної системи диференціальних рівнянь зі сталими коефіцієнтами?

Дата добавления: 2014-01-14