Графические способы расчета водохранилища

В графических способах расчетов водохранилищ применяют интегральные (суммарные) кривые объемов стока и отдачи или их разности.

Полные интегральные (суммарные) кривые. Для построения полной интегральной кривой стока используют гидрограф стока. Площадь элементарной гидрографа с основанием dt и высотой Q дает элементарный объем

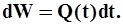
(17)

Объем стока за время t получаем интегрированием уравнения (17), т.е.

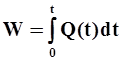
(18)

Таким образом, вычисляя интеграл (18), последовательно за интервал времени t₁, t₂ ..., t_N соответственно получаем объем стока W₁, W₂,..., W_N. Откладывая их в прямоугольной системе координат, получаем кривую, характеризующую изменение суммарного стока за рассматриваемый период. Эта кривая и носит название полной интегральной кривой стока.

При конечных интервалах времени объем стока за интервал Dt_i равна:

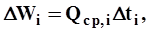
(19)

асуммарный сток

,

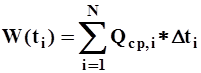(20)

где Q_ср,i - средний расход за интервал времени Dt_i.

Полная интегральная кривая имеет следующие свойства:

ордината кривой представляет суммарный сток за период от начала водохозяйственного года (начало координат) до рассматриваемого мометна времени;

разность ординат двух точек кривой равна объему стока за интервал времени между ними Dt_i;

тангенс угла наклона j к оси абсцисс линии, проходящей через две точки кривой А и B (секущей), характеризует средний расход 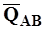в интервале времени Dt между этими точками;

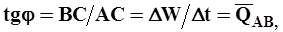
(21)

а тангенс угла j_А наклона к оси абсцисс касательной 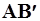определяет расход Q_A в точке касания:

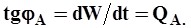
(22)

При использовании зависимостей (21) и (22) для вычисления расходов воды необходимо учитывать масштабы построения интегральной кривой. Обозначив масштаб объемов через m_w, а масштаб времени - через m_t, длина отрезков ВС и АС на рисунке 1в, представим в виде 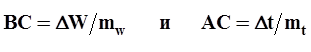. Подставляя найденные значения в формулу (21), получаем

`,

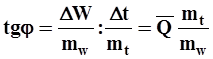(23)

откуда следует, что

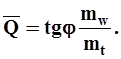
(24)

Полную интегральную кривую можно построить на основе предварительно составленной таблицы.

При водохозяйственном расчете водохранилища на одном чертеже совмещают полную интегральную кривую стока W(t) и полную интегральную кривую отдачи U(t). Кривые строят в одном масштабе, начиная с момента, соответствующего опорожнению водохранилища до мертвого объема V_умо.

Сопоставляя интегральные кривые стока и отдачи (потребления), находят избыток, дефициты, полезный объем и другие показатели регулирования стока. Полные интегральные кривые используют в основном при расчетах без учета потерь воды, так как учесть потери графически сложно и снижается точность вычислений.

Рассмотрим наиболее простой случай - однотактную работу водохранилища при постоянной в течение всего периода регулирования отдаче (рис. 2). Сопоставление интегральных кривых стока W(t) и отдачи U(t) позволяет установить следующее.

1. Суммарный объем стока W за расчетный период превышает суммарное потребление U за этот же период ((DF > EF). Разность конечных ординат кривых стока и отдачи равна суммарному сбросу V_сб.

2. В начальный период регулирования от момента времени t₀ до t₁ наклон к оси абсцисс кривой стока W(t) больше, чем наклон кривой отдачи U(t), следовательно, согласно свойствам интегральных кривых сток Q превышает отдачу q.

Проведя верхнюю касательную к кривой стока, параллельную кривой отдачи U(t), находим момент t₁, окончания избыточного стока и перехода к периоду дефицита. Суммарный избыток за время от t₀ до t₁ равен разности ординат кривых стока и отдачи, соответствующих точке верхнего касания, то есть DV₁ = АС-ВС.

3. С момента t₁ (точка верхнего касания А) до конца расчетного периода t₂ наклон кривой W(t) меньше наклона кривой U(t); очевидно в течение этого периода расход притока Q меньше расхода отдачи q и имеет место дефицит. Нижняя касательная, проведенная к кривой стока параллельно кривой отдачи, определит окончание дефицита (точка D), а вертикальное расстояние между предыдущей верхней и последующей нижней касательной - суммарный объем дефицита Dd за период от t₁ до t₂.

4. Поскольку в рассматриваемом случае других дефицитов нет, найденный объем дефицита Dd и будет соответствовать объему водохранилища, необходимому для регулирования стока, то есть полезному объему W_плз.

Следовательно, при однотактной работе водохранилища полезный объем W_плз равен вертикальному расстоянию между касательными, проведенными параллельно интегральной кривой потребления в начале дефицита (верхняя касательная) и в конце его (нижняя касательная).

Разностная интегральная кривая. При графических расчетахводохранилищ сезонного регулирования стока применяют также разностную интегральную (суммарную) кривую, которая характеризует непрерывный ход изменения разности суммарных объемов, стока и отдачи во времени:

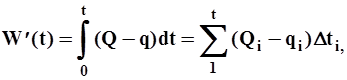
(25)

где 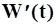- ордината разностной интегральной кривой стока и отдачи; Q и q - расход притока и отдачи, м³/сек.

Выражение (25) можно представить и в другом виде:

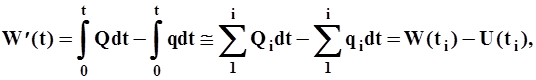
((26)

из которого следует, что ординаты разностной интегральной кривой представляют собой разность ординат полной интегральной кривой стока W(t) и полной интегральной кривой отдачи U(t).

Разностную интегральную кривую строят в прямоугольных координатах откладывая по оси абсцисс время t и по оси ординат .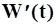

Основные свойства разностной кривой следующие.

1. Ординаты разностной интегральной кривой равны разности суммарных объемов стока и отдачи за период от начала расчета до рассматриваемого момента.

2. Разность ординат двух точек кривой равна разности приращений стока и отдачи за время dt:

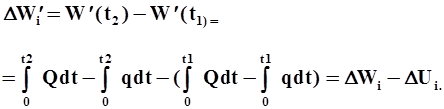
(27)

3. Тангенс угла наклона к оси абсцисс секущей, проведенной через две точки разностой кривой, характеризует разность расходов притока и отдачи за рассматриваемый интервал времени

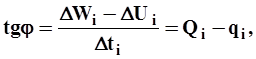
(28)

а тангенс угла наклона касательной соответствует разности расходов притока и

отдачи для момента точки касания:

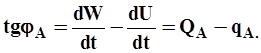
(29)

Отсюда следует, что если тангенс угла наклона касательной или секущей положительный, то Q_i > q_i , и, наоборот, если тангенс отрицательный, то Q_i < q_i; при Q_i= q_i тангенс угла равен нулю - разностная кривая имеет максимум или минимум. Очевидно, что в тот период, когда разностная кривая имеет подъем (тангенсы угла наклона касательных положительные),наблюдается избытки, а когда кривая имеет спад (тангенсы отрицательные), - дефициты; в верхней экстремальной точке (максимум) осуществляется переход от избыточного стока к дефициту, а в нижней (минимум) - от периода дефицитов к периоду избыточного стока. Полезный же объем водохранилища V_плз определяется как наибольшая разность ординат предыдущей максимальной и последующей минимальной экстремальных точек разностной интегральной кривой.

Дата добавления: 2014-01-14