В.3. Базовые фрагменты схем алгоритмов

В теоретическом плане [3] СА – это ориентированный граф (совокуп-ность вершин и связей между ними), вершины которого могут быть одного из трёх типов (рис. В.1):

· функциональная (используется для представления функции f: X→Y, т. е. арифметического выражения);

· предикатная (используется для представления предиката p: X→{FALSE (ложь), TRUE (истина)}, т. е. логического выражения, опреде-ляющего управление по одной из возможных ветвей);

· объединяющая (реализует передачу управления от одной из двух входных ветвей к одной выходной ветви).

Отметим, что в практике объединяющие вершины не выделяются (они ясны по умолчанию).

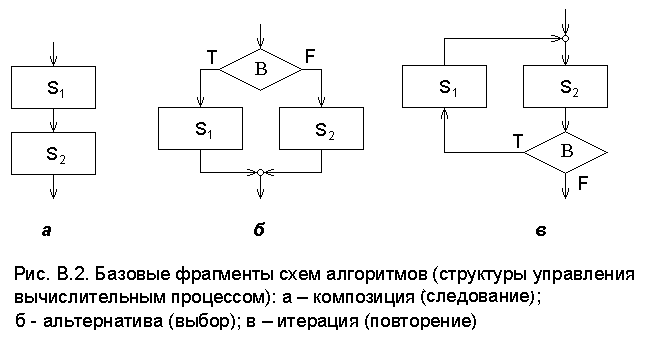
Из данных вершин графа составлены (рис. В.2) простейшие струк-туры управления вычислительным процессом (базовые фрагменты СА). Здесь В интерпретируется как булево выражение, а S₁ и S₂ – как прог-раммные операторы (процедуры). Схема на рис. В.2,а называется компо-зицией (следованием) и записывается в виде S₁; S₂. Схема на рис. В.2,б называется альтернативой (выбором) и записывается в виде if B then S₁ else S₂; в частном случае S₂=Æ получается часто используемый сокращён-ный оператор if B then S₁. Схема на рис. В.2,в[3] называется итерацией (циклом или повторением); получили распространение 3 частных случая:

1) S₂ = Æ. Этому случаю соответствует оператор while B do S₁.

2) S₁ = Æ. Этому случаю соответствует оператор do S₂ while B или, в эквивалентной форме, оператор repeat S₂ until .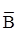

3)

S₁ = S₂ = Æ. Схема вырождается в ждущую вершину (ждущие вершины используются в СА процессов, управляющих событиями).

Теоретически было показано [3], что любая СА может быть сос-тавлена путём суперпозиции базовых фрагментов СА, изображённых на рис. В.2 (теорема Дейкстра). Поскольку каждый из базовых фрагментов имеет один вход и один выход, то у любой СА, составленной из этих фрагментов, также будет один вход и один выход. СА, в которой используются только базовые фрагменты, называется структурированной. Этот же принцип (один вход и один выход) лежит в основе структурного программирования.

Итак, совокупность трёх структур управления процессом вычислений достаточна для построения любой СА. Но СА, полученная путём суперпо-зиции этих структур, не обязательно будет простейшей или наиболее естественной. Поэтому в практике допускается некоторое расширение базового набора структур управления. Например, в некоторых случаях удобнее использовать оператор множественного выбора (типа case … of).

Допускается также преждевременный выход из цикла – операторы while…do и repeat…until, аккуратное применение оператора goto и др. Во всех этих случаях выдерживается основной принцип управления про-цессом вычислений – структура СА должна иметь один вход и один выход.

В практике при начертании схем алгоритмов применяют большое разнообразие вершин с целью получения более наглядных схем, чем это достижимо при использовании только базовых фрагментов; основные вершины СА и правила их соединения приведены в прил. А.

В зависимости от характера связи между вершинами СА алгоритмы делятся на линейные, ветвящиеся, циклические.

В гл. 1 рассматриваются соответствующие примеры.

Контрольные вопросы

1. В каких случаях вычислительный процесс не является алгоритмом?

2. В чём суть проблемы алгоритмической неразрешимости? Почему проблема алгоритмической неразрешимости более трудная, чем проблема алгоритмической разрешимости?

3 Из чего следует необходимость уточнения понятия алгоритма? Каковы подходы к его уточнению?

4. Какие виды обработки данных знаете Вы?

5. Каковы формы представления алгоритмов? Что у них общего и чем они отличаются?

6. Какие основные блоки, используемые в СА, Вы знаете?

7. Какова последовательность действий при решении задачи на ЭВМ?

8. Что такое структуры управления вычислительным процессом? Как они связаны с базовыми фрагментами СА?

9. Какие виды вычислительных процессов и алгоритмов Вы знаете?

10. Чем отличается тестирование программы от её отладки?

11. Как Вы понимаете неоднозначность СА? Что означает термин ²интерпретация² СА?

[1] Диофантово уравнение имеет вид xⁿ + yⁿ = zⁿ, где n – целое. Требуется найти целочисленное решение для произвольного n. Найти такое решение в общем виде не удаётся.

[2] Существует теорема о том, что для раскраски любого планарного графа необходимо не более чем 4 краски. Однако доказать эту теорему в общем виде не удаётся.

[3] Строго говоря, схема рис. В.2,в не является структурой управления, так как использует оператор goto.

Дата добавления: 2014-01-14