Теоретическое обоснование метода простых итераций

Определение 2.4. Отображение 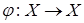называют сжатым отображением в себе, если для любых x, y, принадлежащих X, выполняется услови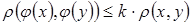е , где .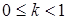

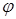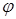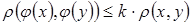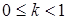Число называется коэффициентом сжатия отображения . Отображение может не быть сжатым на всем пространстве , а лишь на некоторой его части , когда неравенство , , выполняется при всех .

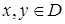Пусть .

Определение 2.5. e -окрестностью точки 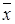называется множество точек x пространства X, которые удовлетворяют условию .

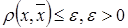Математическая запись этого определения выглядит следующим образом: .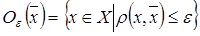

Определение 2.6. Неподвижной точкой отображения 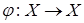называется такая точка 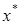, что .

Замечание. Если представить уравнение 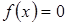в виде , то решение уравнения сведется к поиску неподвижной точки отображения .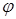

Теорема 2.3. Если отображение 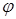является сжатым и имеет неподвижную точку 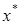, то любая e -окрестность неподвижной точки отображается сама в себя, то есть 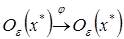, для любого .

Доказательство.

Пусть дана – произвольная e -окрестность точки 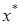, и пусть точка 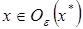– произвольная точка из этой окрестности.

Докажем, что также принадлежит . Действительно, по определению сжатых отображений можно записать

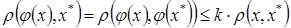, где .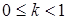

, так как 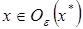, учитывая, что 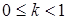, можно утверждать, , то есть .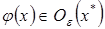

Принцип Банаха сжатых отображений устанавливает достаточное условие существования и единственности неподвижной точки сжатого отображения 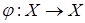, когда X является полным метрическим пространством.

Теорема 2.4. (Принцип Банаха.) Пусть 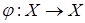– сжатое отображение полного метрического пространства X в себя с коэффициентом сжатия k. Тогда 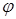имеет одну неподвижную точку 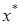, причем

1. 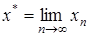, где 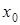– произвольная точка пространства X и

2. имеет место оценка для всех n:

.

Доказательство.

I. Докажем, что существует не более одной неподвижной точки.

Допустим противное, то есть пусть существуют точки и 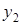такие, что , 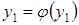и 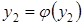. Тогда

.

Получили противоречие, так как условие 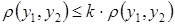, при 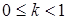выполняться не может. Наше предположение было неверно.

II. Докажем фундаментальность последовательности .

Не нарушая общности рассуждений, будем считать, что 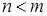, оценим .

.

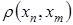Последнее равенство получается по формуле суммы бесконечной геометрической прогрессии с первым членом, равным 1: 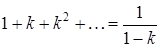, при . .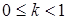

Так как 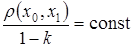, 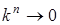при , то отсюда следует, что 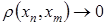, при . То есть – фундаментальная последовательность.

Так как X – полное метрическое пространство, то последовательность имеет в X предел, который мы обозначим через .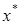

III. Докажем, что 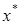– неподвижная точка. Отображение , будучи сжатым отображением, является непрерывным отображением. В равенстве 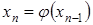перейдем к пределу, получим 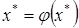, то есть 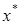– неподвижная точка отображения .

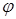IV. Докажем теперь оценку .

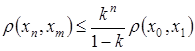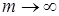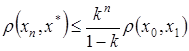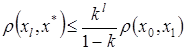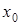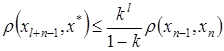Ранее было доказано, что . Перейдем в этом неравенстве к пределу при . Получим . Переобозначим: . Так как за начальное приближение можно взять любую точку из X, возьмем в качестве значение (-ое приближение), тогда , . Имеем таким образом . Это неравенство верно при любом натуральном l, а значит и при , то есть .

Теорема доказана полностью.

Замечание. Принцип Банаха сжатых отображений имеет очень важное значение. Он утверждает, что если является сжатым отображением полного метрического пространства в себя, то неподвижную точку этого отображения можно найти с любой степенью точности, построив итерационную последовательность , , ,..., , ….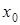

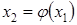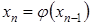Оценить степень приближения можно так:

,

то есть если нужно найти приближение к неподвижной точке с точностью e, то следует строить итерационный процесс до тех пор, пока расстояние между двумя приближениями не станет меньше .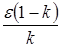

Дата добавления: 2014-01-14