С трехдиагональной матрицей

Метод прогонки решения систем алгебраических уравнений

Достаточные условия применимости метода прогонки.

С трехдиагональной матрицей.

Лекция 10.

«Метод прогонки решения систем алгебраических уравнений

Итерационные методы. Метод простых итераций.»

Метод прогонки является модификацией метода Гаусса для частного случая разряженных систем трехдиагональной матрицы, которые возникают при моделировании некоторых инженерных и краевых задач.

Рассмотрим следующую задачу:

, (3.1)

где , , 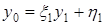, , 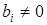для всех . Матрица этой системы

содержит нули везде кроме главной диагонали и двух соседних и является трехдиагональный. Это система линейных алгебраических уравнений относительно величин , , …, .

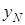Будем находить неизвестные по следующей формуле: 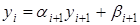(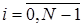) с неизвестными коэффициентами прогонк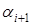и и 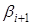(). Подставим 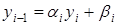в (3.1).

,

,

,

.

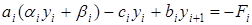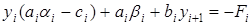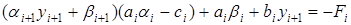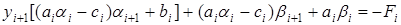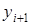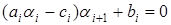Так как это равенство выполняется для любого , то и . Итак для

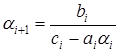(3.2)

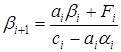(3.3)

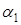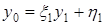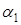Это прогоночные коэффициенты. Для определения и заметим, что и . Отсюда видно, что и . Зная и , из (3.2) и (3.3) определим все прогоночные коэффициенты. Этот процесс называется прямым ходом прогонки: .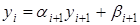

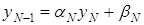Далее заметим, что по условию . С другой стороны . Итак

, .

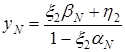Теперь, зная 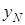, можно найти все (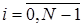). Этот процесс называется обратным ходом прогонки.

Метод прогонки является точным методом, а, следовательно, результат, отвлекаясь от погрешностей вычислений, можно считать точным.

Дата добавления: 2014-01-14