Эффективность двоичных кодов БЧХ

Для оценки эффективности кодов БЧХ воспользуемся теоремой 5.1, позволяющей установить соотношение между корректирующей способностью кода и его параметрами n и k.

Пусть для циклического (n, k) – кода справедливо 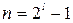для некоторого l, откуда .

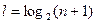Тогда кратность исправляемых ошибок этим кодов определяется как

.

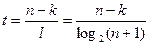Минимальное кодовое расстояние может быть найдено из известного соотношения

.

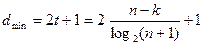Этих сведений достаточно для краткого анализа эффективности циклического кода в реальном канале с известными параметрами р и α.

Для режима исправления ошибок выигрыш по достоверности по сравнению с простым кодом равен

.

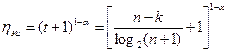Для режима обнаружения ошибок выигрыш составляет

.

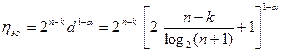Существенным является тот факт, что при исправлении ошибок теоретически возможно обеспечение любой степени повышения достоверности за счет увеличения длины кода n и числа избыточных элементов n - k. Однако практическая реализация таких кодов вызвала бы серьезные затруднения.

Рассмотрим пример.

Пример 6.12. Пусть некоторый реальный канал характеризуется параметрами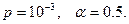

Найти циклический (n, k) – код, повышающий достоверность передачи на 1 десятичный порядок путем исправления ошибок, т.е. требуется найти код, для которого

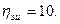
Определим сначала необходимое количество избыточных элементов . Составим уравнение:

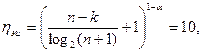
откуда

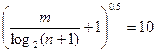
или

.

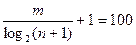Потребное число избыточных элементов

.

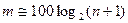Для нахождения кода с данным числом избыточных элементов составим таблицу

N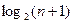

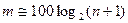
Из построенной таблицы видно, что требуемой эффективностью обладают коды с п >1000.

В частности, данной эффективностью обладают коды (1023, 10) и (1023,20), для которых эффективность равна

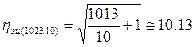
и

.

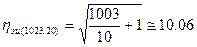Сравнение значения для 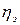в режимах исправления и обнаружения позволяет сделать вывод, что режим обнаружения эффективнее исправления для одного и того же кода и канала в 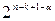раз. Например, для кода (1023,10) из предыдущего примера эффективность при обнаружении ошибки равна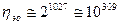

Дата добавления: 2014-01-14