
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коды для исправления пачек ошибок
|
|
|
|
Задачи
Задачи
1. Построить все циклические коды на основе разложения двучлена 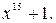 Ниже приведены сомножители и последовательности степени их корней.
Ниже приведены сомножители и последовательности степени их корней.
Сомножитель Степени корней
x+1 0=15
x4+x+1 1 2 4 8
x4+x3 +x2 +x+1 3 6 9 12
x2+x+1 5 10
x4+x3 +1 7 11 13 14
2. Определить корректирующие свойства циклического (15,11) – кода
а) с g(x)=1+x+x4;
б) с g(x)=1+x3+x4;
в) с g(x)=1+x+x2+x3+x4.
3. Определить корректирующие свойства циклического (15,7) – кода
а) с g(x)=(1+x+x4)(1+x3+x4);
б) с g(x)=(1+x+x4)(1+x+x2+x3+x4)
в) с g(x)=(1+x3+x4)(1+x+x+x2+x3+x4)
4. Построить порождающую матрицу и матрицу проверок для укороченного циклического (10,5) – кода, полученного из (15,10) – кода с g(x)=(1+x)(1+x+x4).
Определить dmin (10,5) – кода.
5. Привести матрицу проверок H(7,4),построенную в примере 5.5 к канонической форме.
6. Показать, что поле GF( 23) с примитивным элементом α, являющимся корнем неприводимого многочлена π(x)= 1 +x+x3, может быть представлено в следующем виде:
| Степень | Многочлен | Вектор |
| α α2 α3 α4 α5 α6 α7=1 | α α2 1 + α α + α2 1 + α + α2 1 + α2 |
7.2. Быстрое декодирование кодов БЧХ
1). Ключевое уравнение
Рассмотрим процедуру быстрого декодирования применительно к кодам Рида-Соломона (PC). Для этих кодов справедлива граница Синглтона:
n-k= d-1=2t,
где n-k — избыточность кодовой комбинации,
d - минимальное кодовое расстояние,
t - кратность гарантированно исправляемых ошибок.
Будем полагать, что код используется в режиме исправления ошибок. Пусть в приемник АПД поступила кодовая комбинация PC-кода
С(x)=f (x)+e(x),
где f(x) - переданная передатчиком АПД кодовая комбинация, в которой в процессе передачи по каналу связи произошло υ ошибок, отображаемых многочленом е(х). Здесь 0≤ v≤t.
Многочлен ошибок можно представить в виде
e (x)=ei1 xi1 +ei2xi2+…+eivxiv=∑eilxil,
где eil - значение ошибки, il - номер позиции кодовой комбинации, в которой произошла ошибка. Для исправления ошибок необходимо определить eil и il. Это возможно выполнить на основе синдрома. Введем понятие синдромного многочлена:
S(x)=S1x0+S2x1+…+Sn-k=2tx2t-1.
Коэффициенты Si определяются подстановкой в С(х) корней αl порождающего многочлена кода PC.
S1=C(x= αl)=f(x= αl)+е(х= αl)=e(αl),
где l≤ l ≤ 2t.
Теперь получим, S1=e1αi1 +e2αi2+…+eivαiv и т.д.
Для упрощения записи компонентов синдромного многочлена определим для всех l =1,...,v значения ошибки Уl= eil, и локаторы ошибок Хl= ail=l,где il=l - истинное положение l-й ошибки.
В этих новых обозначениях S1 запишется в виде:
S1=Y1X1+ Y2X2+…+ YyXy.
Здесь Yl и Хl - элементы поля GF(q) над которым построен PC-код, а α - примитивный элемент этого поля. В результате получим следующую систему из 2t уравнений относительно υ неизвестных локаторов X 1,..., Xv и v неизвестных значений ошибок Y1,..., Yυ:
S1=Y1X1+ Y2X2+…+ YvXv,
S2=Y1X12+ Y2X22+…+ YvXv2,
...
S2t=Y1X12t+ Y2X22t+…+ YvXv2t.
В силу определения синдрома эта система уравнений должна иметь хотя бы одно решение. В теории кодирования доказано, что это решение единственно. Изложение известных алгоритмов поиска этого решения базируется на понятии ключевого уравнения.
Для его формирования вводятся еще два многочлена:
1. Многочлен локаторов ошибок
Λ(х)=1+ Λ1х+Λ2 х2+ Λvxv, имеющий корни, обратные локаторам ошибок Xl-1, l=1…,v. Это позволяет представить Λ (x) в следующем виде:
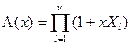
2. Многочлен значений ошибок. Он определяется через S(x) и Λ(х) в соответствии с видом введенного выше многочлена ошибок
Ω(x)=S(x)* Λ (x) (mod x2t)
Выражение для Ω(х) определяет множества из 2t-v уравнений и называется ключевым уравнением, так как оно является ключом решения задачи декодирования.
Ключевое уравнение позволяет получить v уравнений для v неизвестных коэффициентов Λ(x). Эти уравнения являются линейными. Они могут быть решены обычными методами, либо с помощью итерационных процедур. После нахождения Λ(х) ключевое уравнение позволяет найти неизвестные компоненты многочлена е (х ) и по ним переданную кодовую комбинацию f(x)=C(x)+e(x).
Из изложенного можно сделать вывод, что декодирование кодов БЧХ на основе решения ключевого уравнения распадается на два этапа.
I этап — вычисление многочлена локатора ошибок Λ(х).Для двоичных кодов БЧХ этим этапом декодирование завершается.
II этап - для недвоичных кодов, какими являются РС-коды, вычисление многочлена значений ошибок Ω(х), позволяющего вычислять значение каждой из υ ошибок в принятой комбинации.
Для нахождения многочлена локаторов ошибок из литературы известны три алгоритма:
1. Алгоритм Питерсона.
2. Алгоритм Берлекемпа-Месси.
3- Алгоритм Евклида - алгоритм СКХН.
Авторы первого и второго алгоритмов указаны в их названии. Алгоритм Евклида для целей решения ключевого уравнения был впервые предложен четырьмя авторами: Сугияма, Касахара, Хирасава и Намекава. В дальнейшем для краткости будем называть алгоритмом Евклида.
Алгоритм Питерсона может быть использован как самостоятельная процедура декодирования недвоичных циклических кодов и на II этапе.
Алгоритм Берлекемпа-Месси и алгоритм Евклида на II этапе декодирования для недвоичных циклических кодов дополняют алгоритмом Форни, позволяющим по корням Λ (х ) и многочлену Ω(x) найти значения ошибок. Сочетание алгоритма Берлекемпа-Месси и алгоритма Форни получило название быстрого декодирования кодов БЧХ.
Рассмотрим сущность изложенных алгоритмов декодирования
2). Решение ключевого уравнения
а). Алгоритм Питерсона.
У. Питерсон [1] представил ключевое уравнение в матричной форме:

Таким образом, задача определения коэффициентов многочлена локаторов ошибок сводится к прямому решению системы v линейных уравнений с v неизвестными.
б) Алгоритм Евклида.
Известно, что, если существует наибольший общий делитель d(x)двух многочленов а(х) и b(х), тосуществуют многочлены f(x) и g(x) такие, что справедливо: a(x)f{x)+b(x)g(x)=d(x).
Многочлен d(x) может быть найден по алгоритму Евклида, который состоит в последовательном делении с остатком а(х) на b(х), затем b(х) на первый остаток r1(х),затем r1(х) на второй остаток r2(х) ит.д.
При декодировании кодов БЧХ интересуются не конечным результатом алгоритма Евклида, а промежуточными результатами, которые можно представить в виде: a(x)f(x)+b(x)g(x)=r(x).
У. Сугияма и его соавторы [3] использовали этот результат для решения ключевого уравнения следующим образом: b(x)g(x)= ri(x) (mod a(x)),полагая,
а(х)=х2t, b(x)=S(x), gl(x)=Λi(x), ri(x)=Ωi(x).
При этом используется свойство алгоритма Евклида:
deg[gi(x)]+deg[ri-l(x)]=deg[a(x)].
Если а(х)=х2t, то deg[Λi(x)]+deg[Ωi-l(x))=2t,
deg[Λi(x)]+deg[Ωi(x))<2t.
При появлении v≤t ошибок имеем: deg[Ω(x)]< deg[Λ (x)] ≤t.
Существует единственный с точностью до постоянного множителя (элемента поля) многочлен Λ(х) степени ≤t, удовлетворяющий уравнению:
Ωi(x) =S(x) Λi(x) (mod x2t),
если deg[Ωi-1(x)]≥t при deg[Λi(x)]≤t
и deg[Ωi(x)]<t при deg[Λi+1,(x)]>t.
Поэтому промежуточные результаты на I-ом шаге дают единственное интересующее нас решение ключевого уравнения.
Таким образом, для решения ключевого уравнения следует применять алгоритм Евклида до тех пор, пока не будет выполнено условие
deg[Ωi(x)]<t.
Итак, алгоритм Евклида решения ключевого уравнения по методу У. Сугиямы и др. сводится к следующему:
1. Применить алгоритм Евклида к а(х)=х2t и b(x)=S(x).
2. Использовать начальные условия:
Λ-1(х)=0,
Λ0(х)=1,
Ω-1(x)=x2t,
Ω0(x)=S(x).
3. Остановиться, если deg[Ωi(x)]<t.
4. Положить Λ(х)= Λi(x) и Ω(x)= Ωi(x).
При вычислении значений Λi(x) и Ωi(x) следует использовать свойство алгоритма Евклида: каждое из значений Λi(x) и Ωi(x) получается из двух предшествующих значений по следующей общей формуле:
Ei(x)=Ei-2(x)+qiEi-1(x),где 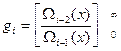
от деления указанных многочленов т,е. многочлен степени 0 и более.
3) Алгоритм Берлекемпа-Месси.
Этот алгоритм был предложен Э. Берлекемпом и Дж. Месси[4] как итеративный процесс построения минимального линейного регистра сдвига с обратной связью, аналогичного схеме решения разностных уравнений, генерирующего все компоненты синдромного многочлена S(x) no υ первым.
Целью алгоритма является нахождение коэффициентов многочлена локаторов ошибок Λ(х), значение которых определяет вид обратных связей регистра.
На рис.7.1 представ л ен доработанный алгоритм, позволяющий кроме А(х) получать также и многочлен значений ошибок и Ω(x).
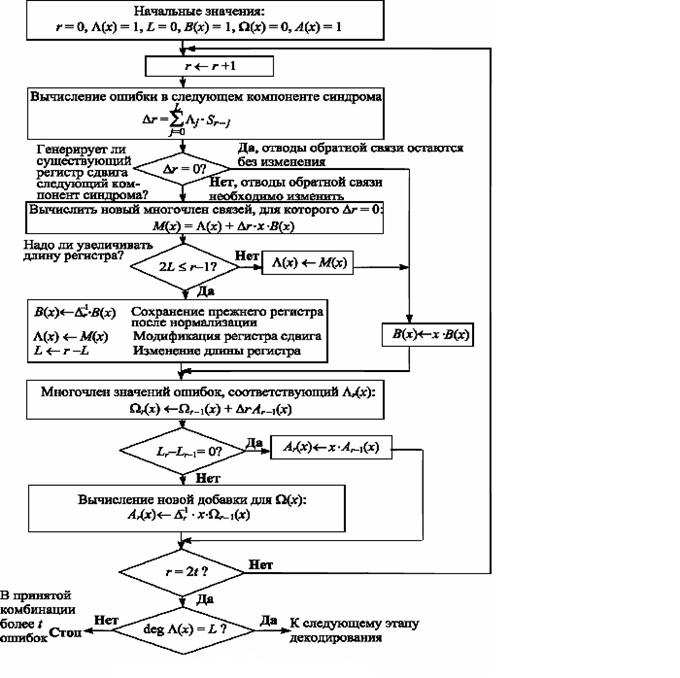
Рис.7.1 Алгоритм Берлекемпа-Месси.
г) Алгоритм Форни.
Д. Форни[4] получил выражение для вычисления значения ошибки, если известны многочлены значения ошибки Ω(x) и локаторов ошибок Λ(х):

Где Хl-1- корень многочлена Λ(х), обратный локатору ошибки Хl, Λl(Х) –производная от Λ(x).
В. Примеры решения ключевого уравнения
Рассмотрим примеры применения рассмотренных алгоритмов для декодирования с исправлением ошибок кодами Рида-Соломона.
Пусть над полем GF(23) с элементами 000, α=1=100, α1=010, α2=001,
α3=110, α4=011, α5=111, α6=101 построен код Рида-Соломона (7,3) с dmin=5, способный исправлять 2-х кратные ошибки. Корнями порождающего многочлена являются следующие элементы GF(23): α1=010, α2=110,α3=110,α4=011.. Порождающий многочлен кода имеет вид;
g(x)=(x+α)(x+α2)(x+α3)(x+α4)=α3+α1x+α0x2+α3x3+x4
Предположим, что по каналу связи была передана комбинация (0000000),а на вход декодера поступила комбинация. f(x)=а2х3 + а5х4. Схема вычисления синдрома определила компоненты синдромного многочлена:
S1=f(x=α)=α5+α2=α3
S2=f(x=α2)=α1+α6=α5
S3=f(x=α3)=α4+α3=α6
S4=f(x=α4)=α0+α0=0
При вычислении значений элементов Si, показатели степеней элементов поля приводятся по mod 7, т.к. для GF(23) а=а7=1. Итак, для принятой комбинации синдромный многочлен имеет вид:
S(x)=α3+α5x+α6x2
Определим для принятой комбинации многочлен локаторов ошибок Λ(х).
Алгоритм Питерсона. Матричное уравнение для нахождения компонентов Λ(х) по S(х) имеет вид:
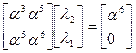
В предложении, что произошло максимальное число исправляемых кодом ошибок t=2 воспользуемся теоремой Крамера [5] для решения системы линейных уравнений, представленных в матричной форме Ах=С, в случае, когда det А существует и отличен от нуля, В этом случае система имеет одно определенное решение, и каждое из неизвестных выражается частным двух определителей, причем в знаменателе стоит определитель |А|, а в числителе, определитель который из него получается заменой коэффициентов при определяемом неизвестном соответствующими свободными членами:
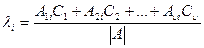
Применяя теорему Крамера для нахождения λ i получаем:
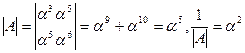

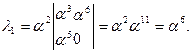
Таким образом, многочлен локаторов ошибок имеет вид:
Λ(x)=1+α6x+α0x2
Корнями многочлена Λ{х) являются элементы GF(23): α3 и α4, т.е. локаторы ошибок
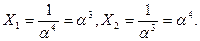
Это дает возможность представить многочлен локаторов ошибок и виде;
Λ(х)=(1+α3х)(1+α4х)
Алгоритм Питерсона позволяет найти также и значения ошибок. Для этого выразим компоненты синдромного многочлена S1 и S2 через локаторы ошибок Xl, и значения ошибок Yl:
S1=Y1X1 + Y2X2
S2=Y1X12 + Y2X2
Представим эти уравнения в матричной форме:
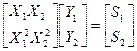
или
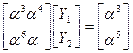
Решим это уравнение тем же способом, каким были найдены λ1 λ2 .Вычислим определитель:
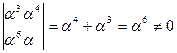
Теперь находим:
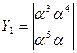 =α(α4+α2)=α5+α3=α2 ,
=α(α4+α2)=α5+α3=α2 ,
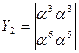 =α(α+α2)=α2+α3=α5
=α(α+α2)=α2+α3=α5
Полученные значения Y1 и Y2 соответствуют коэффициентам многочлена ошибок.
2.Алгоритм Евклида
Поиск значений Λi(x) в Ωi(x), удовлетворяющих приведенным выше критериям, представим в виде таблицы.
| i | -1 | ||
| Λi(x) | α+х+αx2=α(1+α6x+x2) | ||
| Ωi(x) | х4 | S(x) | α 4+α 4х=α(α3+α3х) |
| qi(x) | ___ | ___ | [X4 /S(x)]=α+x+αx2 |
Из приведенной таблицы видно, что найденное значение Λ (х)=α(1+ α6x+x2) отличается от Λ (х), подученного по алгоритму Питерсона постоянным сомножителем α. Понятно, что корни этих многочленов совпадают, т,е, постоянный сомножитель не влияет на определение локаторов ошибок.
3, Алгоритм Берлекемпа-Месси. Вычисление Λ(х) и Ω(x) в соответствии с доработанным алгоритмом Берлекемпа-Месси представим ввиде следующей таблицы:
| r | Sr | Δr | M(x) | B(x) | Λ(x) | L | Ω(x) | A(x) |
| 0 | 1 | 1 | 0 | 0 | 1 | |||
| 1 | α3 | Α3 | 1+α3x | α4 | 1+α3x | 1 | α3 | 0 |
| 2 | α5 | Α | 1+α2x | a4x | 1+α2x | 1 | α3 | 0 |
| 3 | α6 | Α2 | 1+α2x+α6x | α5+x | 1+α2x+a6x2 | 2 | α3 | αx |
| 4 | 0 | Α2 | 1+α6x+x2 | α5x+x2 | 1+α6x+x2 | 2 | α3+ α3x | αx |
Найденному значению Λ(х) соответствует регистр сдвига с обратными связями, определенными Λ(х), длины L=2, способный вычислять лее компоненты симдромного многочлена по 2-м младшим.
Этот регистр имеет вид:

В исходном состоянии в ячейках памяти регистра записаны компоненты синдрома S1=α3 и S2=α5. По второму такту S2=α5 поступает на выход, а в ячейках остаются S3=α6 и S4=0, которые за два следующих такта поступают на выход.
4. Алгоритм Форни.
Для вычисления значений ошибок необходимо знание Λ(х) и его корней, а также должен быть известен многочлен Ω(x).Непосредственным вычислением находим: ■
Ω(x)=S(x)Λ(x)(modx2t)=(α3+α5x+а6х2)(1+α6x+x2)(modx4)=α3+α3х. Расчетные значения Λ(х) и Ω(x)полностью совпадают с полученными по алгоритму Берлекемпа-Месси и отличаются постоянным сомножителем при вычислении по алгоритму Евклида.
Для нахождения значений ошибок по алгоритму Форни найдем Λ (х)=а6. Подставляя в Ω(х) вместо x значения корней Λ(x)получаем:
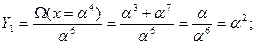
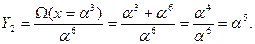
Итак,вычисленное значение многочлена ошибок е(х)= α2x3+α5x4 полностью совпадает с принятой комбинацией f(х) и, следовательно, по каналу связи передавалась комбинация (0000000).
1. Построить кодирующее устройство для укороченного циклического кода (10,5) с 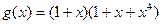 и проследить по тактам процесс формирования избыточных элементов для какой-либо комбинации. Результат проверить алгебраически.
и проследить по тактам процесс формирования избыточных элементов для какой-либо комбинации. Результат проверить алгебраически.
2. Построить устройство обнаружения ошибок (схему вычисления синдрома) для укороченного (10,5) – кода с 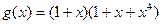 .
.
3. С помощью схемы вычисления синдрома предыдущей задачи определить принадлежность комбинаций 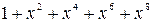 и
и  коду (10,5).
коду (10,5).
4. Построить кодирующее устройство для кода (15,5) с 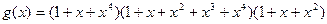 .
.
5. Построить генератор последовательности длины 7 и получить эту последовательность.
6. Построить кодирующее устройство для кода Рида-Соломона(7,5) на основе схемы рис 6.10.
7. Построить генератор элементов поля GF(24)
8. Построить генератор элементов поля GF(25)
ТЕМА 9. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ КЛАССЫ КОДОВ. СОСТАВНЫЕ КОДЫ.
Под пачкой ошибок длины l будем понимать последовательность ошибок, занимающую l последовательных элементов кодовой комбинации, при условии, что первый и последний элементы в этой последовательности искажены.
По аналогии под пачкой в кодовой комбинации будем называть некоторую ее часть, ограниченную с обеих сторон единицами.
Вполне понятно, что некоторый (n, k) – код обладает способностью обнаруживать или исправлять пачки ошибок длины l и менее тогда и только тогда, если его кодовые комбинации не содержат в своем составе пачек данной длины.
С помощью простых рассуждений можно установить минимальное число избыточных элементов в кодовой комбинации группового кода, способного обнаруживать все пачки ошибок длины l и менее.
Во-первых, необходимо, чтобы такой код не содержал пачек длины l и менее. Определим, когда это возможно. Рассмотрим разложение группы, составленной из п – элементных векторов не смежные классы по подгруппе, образующей данный (n, k) – код. Если кодовые комбинации не содержат пачек длины l и менее, то в одном и том же смежном классе не могут существовать 2 комбинации, в которых, начиная с одного и того же разряда, размещены пачки длины l и менее, так как в противном случае их сумма, являющаяся кодовой комбинацией, должна содержать пачку длины меньшей l.
Так как для некоторого фиксированного разряда кодовой комбинации можно указать 2 l различных комбинаций, которые в силу сказанного выше должны принадлежать различным смежным классам, то число смежных классов не может быть меньшим 2 l.
Таким образом, доказано следующее свойство групповых кодов.
Свойство 9.1. Групповой код, обнаруживающий все пачки ошибок длины l и менее, должен содержать, по крайней мере, l проверочных символов.
В случае циклического кода эта нижняя граница для числа проверочных символов является точной. Действительно, любая кодовая комбинация циклического кода может быть представлена как произведение  где g(x) – порождающий многочлен кода степени n-k. Значит каждая кодовая комбинация циклического кода содержит или пачку длины n–k +1 (комбинации
где g(x) – порождающий многочлен кода степени n-k. Значит каждая кодовая комбинация циклического кода содержит или пачку длины n–k +1 (комбинации 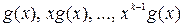 ) или линейную комбинацию циклически сдвинутых пачек длины n–k +1, сумма которых всегда дает пачку большей длины, т.е. справедливо следующее свойство.
) или линейную комбинацию циклически сдвинутых пачек длины n–k +1, сумма которых всегда дает пачку большей длины, т.е. справедливо следующее свойство.
Свойство 9.2. Любой циклический (n, k) – код обнаруживает все пачки ошибок длины (n - k) и менее.
В случае исправления пачек ошибок можно аналогичными рассуждениями получить нижнюю границу для числа проверочных элементов. Действительно, пусть известно, что групповой (n, k) – код исправляет все пачки ошибок длины b. Значит общее число смежных классов в таблице декодирования должно быть не меньше, чем число возможным пачек длины b. В комбинации длины п возможно всего п пачек длины 1, п -1 пачек длины 2, 2(п -2) пачек длины 3 и т.д. Общее число пачек длины b в комбинации длины п равно 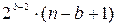 . Таким образом, число смежных классов равно
. Таким образом, число смежных классов равно

Используя формулу для арифметико-геометрической прогрессии, данное выражение прообразуем к виду
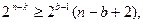
откуда, логарифмируя по основанию 2, получаем 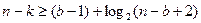 . Итак, справедливо следующее свойство групповых кодов.
. Итак, справедливо следующее свойство групповых кодов.
Свойство 9.3. Число проверочных элементов (n, k) – кода, исправляющего все пачки ошибок длины b и менее равно самое меньшее 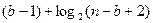 .
.
Одним из самых обширных из известных в настоящее время классов кодов, специально предназначенных для исправления пачек ошибок, являются коды Файра.
Коды Файра – циклические коды, порождающий многочлен которых имеет вид 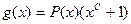 , где Р(х) – неприводимый многочлен степени r, входящий в разложение
, где Р(х) – неприводимый многочлен степени r, входящий в разложение 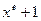 и не являющийся сомножителем никакого двучлена меньшей степени.
и не являющийся сомножителем никакого двучлена меньшей степени.
Необходимо при этом, чтобы с не делилось на е. Длина кодовой комбинации п равна наименьшему общему кратному чисел е и с, т.к. только в этом случае g(x) делит 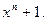
Число проверочных элементов равно 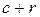 , а число информационных
, а число информационных 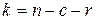 . В [1] показано, что коды Файра исправляют любую одиночную пачку ошибок длины b или меньше и одновременно обнаруживают любую пачку ошибок длины
. В [1] показано, что коды Файра исправляют любую одиночную пачку ошибок длины b или меньше и одновременно обнаруживают любую пачку ошибок длины 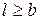 или меньше, если выполняются соотношения
или меньше, если выполняются соотношения  и
и 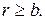 Если применять эти коды только для обнаружения ошибок, то можно обнаружить любую комбинацию из двух пачек ошибок, длина наименьшей из которых не превосходит r, а сумма длин которых не превосходит с+ 1, а так же и любую одиночную пачку ошибок, длина которой не превосходит числа проверочных символов с+r.
Если применять эти коды только для обнаружения ошибок, то можно обнаружить любую комбинацию из двух пачек ошибок, длина наименьшей из которых не превосходит r, а сумма длин которых не превосходит с+ 1, а так же и любую одиночную пачку ошибок, длина которой не превосходит числа проверочных символов с+r.
Указанные свойства кодов Файра обусловлены видом порождающего многочлена. Наличие в g(x) сомножителя 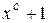 достаточно дл я обнаружения одиночной пачки ошибок длины с. Дополнительная информация, требуемая для определения положения пачки ошибок, обеспечивается сомножителем Р(х).
достаточно дл я обнаружения одиночной пачки ошибок длины с. Дополнительная информация, требуемая для определения положения пачки ошибок, обеспечивается сомножителем Р(х).
Пример 9.1. Код Файра порождается многочленом 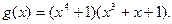 Определить параметры кода и его корректирующие свойства.
Определить параметры кода и его корректирующие свойства.
Здесь r =3, е =7, с =4, n-k=r+c= 7;
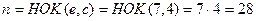
Итак, 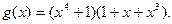 порождает код Файра (28,21). Данный код может исправить пачки ошибок длины b =2 и b =1, а также дополнительно обнаружить при этом пачки длины b =3 и b =4 соответственно. Если использовать этот код только для обнаружение ошибок, то модно обнаружить любую одиночную пачку ошибок длины 7 и комбинацию из двух пачек ошибок, из которых одна не превосходит 3, а сумма длин обоих равна 5 или менее.
порождает код Файра (28,21). Данный код может исправить пачки ошибок длины b =2 и b =1, а также дополнительно обнаружить при этом пачки длины b =3 и b =4 соответственно. Если использовать этот код только для обнаружение ошибок, то модно обнаружить любую одиночную пачку ошибок длины 7 и комбинацию из двух пачек ошибок, из которых одна не превосходит 3, а сумма длин обоих равна 5 или менее.
Для оценки эффективности кодов Файра необходимо знать функцию распределения пачек различной длины в кодовых комбинациях. Поскольку этот вопрос выходит за рамки данного учебного пособия, то эффективность данных кодов строго оценена быть не может. Приближенная оценка может быть произведена при пересчете пачек на кратности ошибок. При таком упрощенном подходе вероятность ошибочного приема кодовой комбинации при одновременном исправлении и обнаружении:
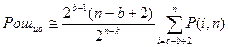
и
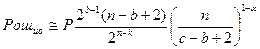 .
.
Для кодов с обнаружением пачек ошибок:
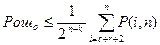
и
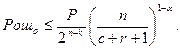
На основании этих формул определяется эффективность кодов. Для случая исправления и обнаружения пачек ошибок
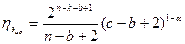 .
.
Для случая обнаружения пачек ошибок
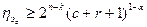 .
.
Из определения кодов Файра вытекает, что при с =1 они совпадают с кодами Хэмминга, имеющими dmin =4, если при этом 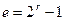 .
.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 547; Нарушение авторских прав?; Мы поможем в написании вашей работы!