Кинетическая энергия

Работа силы (механическая работа)

Мощность

Закон сохранения полной механической энергии

Потенциальная энергия

Кинетическая энергия.

Работа силы (механическая работа)

Тема Закон сохранения энергии

САМОЕ ВАЖНОЕ В ШЕСТОЙ ГЛАВЕ

Вопросы

1. Существуют суда с водометным дви­гателем, выбрасывающим из корабля водя­ную струю. При этом корабль движется в сторону, противоположную направлению движения струи. Является ли движение корабля реактивным движением?

2, При выстреле из ружья стрелок ощущает удар приклада (отдача). Можно ли движение приклада считать реактивным?

3. Ракета может получить ускорение в космическом пространстве, где вокруг нее нет никаких тел. Между тем для уско­рения нужна сила, а сила — это действие одного тела на другое. Почему ускоряется ракета?

4. От чего зависит скорость ракеты?

2. Как осуществляется торможение кос­мического корабля?

Наряду со скоростью важной характеристикой движения яв­ляется импульс тела — векторная величина, равная произведе­нию массы тела на его скорость.

Результат действия силы на тело — изменение его импульса. Изменение импульса тела равно импульсу силы — произведению силы на время ее действия.

Один и тот же импульс силы сообщает разным телам (телам с различной массой) различные скорости, но одинаковые импульсы.

Импульс — одна из немногих сохраняющихся величин. Закон сохранения импульса состоит в том, что полный импульс всех тел, составляющих замкнутую систему, остается неизменным при любых движениях и любых взаимодействиях тел системы.

ГЛАВА 7

Величина, которую мы назвали работой силы (или просто работой), была введена в механику лишь в XIX в., почти через 150 лет после открытия Ньютоном законов движе­ния. Появилась она, когда широко стали применять всевозможные ма­шины. Ведь о действующей маши­не говорят, что она «работает».

С понятием «механическая рабо­та» мы уже встречались в курсе физики VII класса. Там мы видели, что когда на движущееся тело действует постоян­ная сила F и тело совершает в направлении действия силы переме­щение s, то, как говорят, сила со­вершает работу A, равную произве­дению модулей силы и перемещения:

A = Fs.

Там же была введена и единица работы джоуль (Дж): за едини­цу работы принимают работу, совер­шаемую силой в 1 Н на пути, рав­ном 1 м:

1 Дж = 1 Н*м.

Сила и перемещение — величины векторные. Но работа равна произ­ведению модулей векторов F и s, а модуль вектора — величина скаляр­ная. Поэтому и работа — скалярная величина. О работе нельзя сказать, что она куда то направлена.

Положительная и отрицательная работа.

В выражении A=Fs, которое определяет работу, F — сила, приложенная к телу (ее модуль). Но на движущееся тело может действовать не одна, а несколько сил. И каждая из них может со­вершать работу. В этом случае F в выражении для работы означает модуль равнодействующей всех сил. Работа же этой равнодействующей равна сумме работ отдельных сил. Равнодействующая, однако, мо­жет быть равна нулю (тело нахо­дится в равновесии). Тогда если тело движется, то прямолинейно и равномерно. Сумма всех сил при этом равна нулю. Значит, равна нулю и суммарная работа всех сил. Но для этого работа одних сил должна быть положительной, дру­гих — отрицательной. Иначе, их сум­ма не может быть равной нулю. Положительной считается работа сил, сонаправленных с перемеще­нием тела, отрицательной — работа сил, направленных противоположно перемещению. Так, при равномер­ном подъеме груза с помощью подъемного крана на груз действует сила натяжения каната, направлен­ная вверх, т. е. вдоль направления движения груза, и сила тяжести, направленная вниз, против движе­ния груза. Работа силы натяжения каната положительна, а работа силы тяжести отрицательна. Так как силы эти по модулю равны, то и работы их одинаковы по модулю и противо­положны по знаку.

Общее выражение для работы силы.

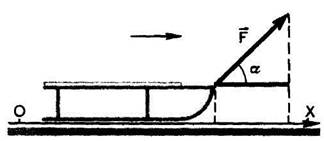
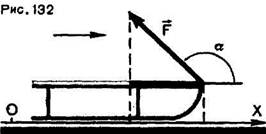
Если направление силы сов­падает с направлением перемеще­ния, то это значит, что угол между векторами силы и перемещения ра­вен нулю. Когда сила и переме­щение противоположны друг другу, угол между этими векторами равен 180°. Но силы, приложенные к дви­жущемуся телу, могут образовывать с направлением перемещения угол, отличный от 0 и 180°. Например, к санкам, движущимся по горизон­тальной дороге в направлении, ука­занном стрелкой (рис. 131, 132), в какой-то момент подействовала сила, направленная под углом а к горизонту. В первом случае (рис. 131) угол а острый, во втором (рис. 132)—тупой. Как вычислить работу, которую совершает сила F, если перемещение санок равно S?

Для этого формулу для работы нужно записать в таком виде:

A = Fs cos α, (1)

где α— угол между векторами силы и перемещения.

В самом деле, если векторы F и s совпадают по направлению, угол между ними равен нулю. Но cos 0° = 1. В этом случае A = Fs. Если векторы F и s направлены противоположно друг другу, то α = 180°, cos 180° = = — 1 и работа А = — Fs. Когда угол α острый (см. рис. 131), его косинус положителен и работа такой силы положительна. Когда угол αтупой (см. рис. 132), его косинус отрицателен и работа силы, направ­ленной таким образом, отрица­тельна.

Работа постоянной силы равна произведению модулей векторов си­лы и перемещения на косинус угла между этими векторами.

Когда работа силы равна нулю.

Направление силы, приложенной к телу, может быть и перпендикуляр­но направлению перемещения тела. В этом случае угол α = 90°, cos 90° = = 0 и работа, как это видно из фор­мулы (1), равна нулю. Так, сила тяжести, которая действует на санки, перпендикулярна направлению дви­жения санок, поэтому она работы не совершает. Не совершает работы и сила, вынуждающая тело двигать­ся равномерно по окружности: она в любой точке траектории перпен­дикулярна направлению скорости тела, т. е. направлению его дви­жения. Например, сила натяжения нити, к которой привязано тело, движущееся по окружности, не со­вершает работы, хотя именно нить заставляет тело так двигаться. Не совершает работы и сила всемир­ного тяготения, под действием ко­торой искусственные спутники Земли движутся по круговой ор­бите.

Рис.131

Вопросы

1. Штангист поднял с помоста штангу и зафиксировал ее над головой. Чему при этом равна работа силы тяжести, дейст­вующей на штангу? Чему равна работа силы упругости мышц штангиста?

2. Штангист поднимает вверх штангу. В чем различие между работой силы упру­гости мышц штангиста и работой силы тяжести?

3. В каком случае сила, приложенная к движущемуся телу, не совершает ра­боту?

4. Тело брошено вертикально вверх. Ка­ков знак работы силы тяжести: а) при подъеме тела; б) при его падении?

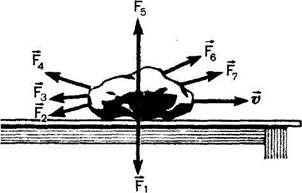
5.На рисунке 133 изображено тело, к которому приложено несколько сил. Чер­ной стрелкой указано направление движе­ния тела. Какие из сил совершают поло­жительную работу, какие — отрицательную?

Упражнение 23

1. На груз, скользящий с трением по горизонтальной поверхности, действует си­ла 200 Н, направленная под углом 60° к горизонту. Чему равна работа силы при перемещении тела, равном 5 м, если дви­жение тела прямолинейное и равномерное? Каков коэффициент трения груза о плос­кость? Масса тела 31 кг.
2. Лыжник массой 70 кг поднимается на подъемнике вдоль склона длиной 180 м, образующего с горизонтом угол 60°. Вы­числите работу силы тяжести, действующей на лыжника. Какой она имеет знак? Какую ра­боту совершает сила натяжения каната подъемника? Скорость подъемника постоян­ная.

Задание

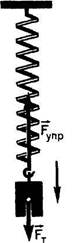
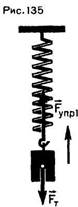
Рассмотрите рисунки 134 и 135 (тело, прикрепленное к пружине, движется вниз, а затем, пройдя наинизшее положение, движется вверх). Выясните: а) в каком случае сила упругости совершает положительную работу, в каком — отрицательную; б) в каком случае работа силы тяжести положительна, в каком — отрицательна?

Рассмотрим тело, к которому приложена постоянная сила F — она может быть и равнодейству­ющей нескольких сил. О силе F можно сказать, во-первых, что она сообщает телу ускорение, т. е. из­меняет его скорость. Во-вторых, что она совершает работу, потому что тело под действием этой силы пере­мещается. Между работой, произведенной силой, и изменением скорости должна поэтому существовать связь. Найдем ее.

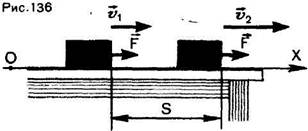
Рассмотрим простейший случай, когда векторы силы и перемещения направлены вдоль одной прямой в одну и ту же сторону. В ту же сто­рону направим и координатную ось (рис. 136). Тогда проекции силы F, перемещения s, ускорения а и скорости v будут равны модулям самих этих векторов.

Напишем для этого случая вы­ражение для работы силы:

A=Fs (1)

и формулу второго закона Ньютона:

F = ma. (2)

Во второй главе мы видели, что при прямолинейном равноускорен­ном движении (в нашем случае дви­жение именно такое, так как сила постоянная) перемещение и скорость тела связаны соотношением

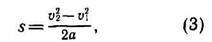
где V_[ и v₂ — модули вектора ско­рости в начале и в конце участка s. Подставив в формулу (1) выраже­ния для F и s из формул (2) и (3), получим А=ma (V₂² – V₁²)

2a

или

A= mV₂² - mV₁²

2 2

Эта формула и связывает рабо­ту силы А с изменением скорости тела (точнее, квадрата скорости).

Выраже­ние в правой части равенства (4) представляет собой изменение величины mv²/2 — половины произведения массы тела на квадрат его ско­рости. Эта величина имеет особое название — кинетическая энергия. Обозначим ее через E_k- Тогда фор­мула (4) примет вид:

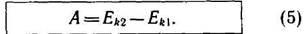
Работа силы (или равнодейству­ющей сил) равна изменению кине­тической энергии тела.

Это утверждение называется тео­ремой о кинетической энергии.

Когда сила, действующая на тело, направлена в сторону движе­ния и, следовательно, совершает положительную работу, то mV₂²>mV₁²

Это означает, что кинетическая энер­гия тела увеличивается. Так и долж­но быть, так как сила, направлен­ная в сторону движения тела, уве­личивает модуль его скорости. По­нятно, что, если сила направлена в сторону, противоположную направ­лению движения тела, она соверша­ет отрицательную работу и кинети­ческая энергия тела уменьшается.

Из формулы (4) видно, что кинетическая энергия выражается в тех же единицах, что и работа, т. е. в джоулях.

Теорема о кинетической энергии была нами получена из второго закона Ньютона. Можно даже ска­зать, что формулы (4) и (5) —это просто иначе записанные формулы второго закона Ньютона. Поэтому теорема о кинетической энергии (5) справедлива независимо от того, ка­кие именно силы приложены к телу: сила упругости, сила тяжести или сила трения.

Таким образом, формула (4) (или (5)) показывает, что если на тело действует сила, то изменяется его кинетическая энергия. А изме­нение кинетической энергии равно работе силы. У любого тела (любой массы) кинетическая энергия изме­нится на одну и ту же величину, если работа силы одна и та же. Большая сила при малом перемещении тела вызовет такое же изменение кине­тической энергии, как малая сила при большом перемещении; если только работа силы, т. е. произ­ведение силы на перемещение, будет одной и той же.

Что характеризует кинетическая энергия тела?

Представим себе, что покоящемуся телу (V_о = 0) массой т требуется сообщить скорость, равную v (например, сообщить ско­рость v покоящемуся в стволе ору­дия снаряду). Для этого сила, при­ложенная к телу, должна совершить определенную работу. Чему равна эта работа? Согласно теореме о ки­нетической энергии,

Следовательно, кинетическая энер­гия тела массой m, движущегося со скоростью v, равна работе, кото­рую нужно совершить, чтобы сооб­щить телу эту скорость. Такую же работу, но противоположного знака нужно совершить, чтобы тело, дви­жущееся с такой скоростью, оста­новить. Из теоремы о кинетической энергии следует также, что [кине­тическая энергия — это физическая величина, характеризующая движу­щееся тело; изменение этой вели­чины равно работе силы, приложен­ной к телу.

Вопросы

1. Что такое кинетическая энергия?

2. В чем состоит теорема о кинети­ческой энергии?

3. Как изменяется кинетическая энергия тела, если сила, приложенная к нему, со­вершает положительную работу? Отрица­тельную работу?

4. Изменяется ли кинетическая энергия тела при изменении направления вектора его скорости?

5. Два шара одинаковой массы катятся навстречу друг другу с одинаковыми по модулю скоростями по очень гладкой по­верхности. Шары сталкиваются, на мгнове­ние останавливаются, после чего движутся в противоположных направлениях с такими же по модулю скоростями. Чему равна их общая кинетическая энергия до столкно­вения, в момент столкновения и после него?

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ

Какую работу нужно совершить, чтобы поезд, движущийся со скоростью V 1 =72 км/ч, увеличил свою скорость до значения V₂ = — 108 км/ч? Масса поезда 1000 т. Какова должна быть сила тяги локомотива, если это увеличение скорости должно произойти на участке длиной 2000 м?

Решение. Для определения работы А используем формулу тео­ремы о кинетической энергии в сле­дующем виде:

A= mV₂² - mV₁²

2 2

Подставив сюда приведенные в за­даче данные, находим:

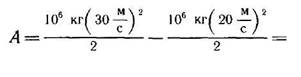
= 2,5-10⁸ Дж.

Если A=Fs, то F= A/s. Следовательно

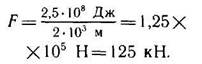
Упражнение 24

1. К покоящемуся телу массой 3 кг при­ложена сила 40 Н. После этого тело про­ходит по гладкой горизонтальной плоскости без трения 3 м. Затем сила уменьшается
до 20 Н, и тело проходит еще 3 м. Найдите кинетическую энергию тела и его скорость
в конце первого участка.

2. Какая работа должна быть совершена для остановки поезда массой 1000 т, дви­жущегося со скоростью 108 км/ч?

3. Вычислите кинетическую энергию искусственного спутника Земли массой 1300 кг,
движущегося по круговой орбите на высоте 100 км над поверхностью Земли.

4.Тело движется равномерно по окружности радиусом 0,5 м, обладая кинети­ческой энергией 10 Дж. Какова сила, дейст­вующая на тело? Как она направлена? Чему равна работа этой силы?

5. Шофер выключил двигатель автомо­биля при скорости 72 км/ч. Пройдя после
этого 34 м, автомобиль остановился. Чему была равна кинетическая энергия автомобиля
в момент выключения двигателя, если сила трения колес о дорогу равна 5880 Н? Ка­кова масса автомобиля?

6. Автомобиль массой 4 т движется со скоростью 36 км/ч. Какой путь прошел
автомобиль до полной остановки, если сила трения колес о дорогу равна 5880 Н?

Задание

Проанализируйте решения задач 5 и 6 и выясните, от какой величины зависит тормозной путь движущегося тела при заданном значении модуля тормозящей силы. Сравните результат анализа с формулой, приведенной в § 37.

Дата добавления: 2014-01-14